|
|
|
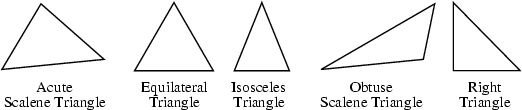
A triangle is a 3-sided Polygon sometimes (but not very commonly) called the Trigon. All triangles are convex. An Acute Triangle is a triangle whose three angles are all Acute. A triangle with all sides equal is called Equilateral. A triangle with two sides equal is called Isosceles. A triangle having an Obtuse Angle is called an Obtuse Triangle. A triangle with a Right Angle is called Right. A triangle with all sides a different length is called Scalene.
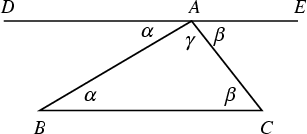
The sum of Angles in a triangle is 180°. This can be established as follows. Let ![]() (
(![]() be Parallel to
be Parallel to ![]() ) in the above diagram, then the angles
) in the above diagram, then the angles ![]() and
and ![]() satisfy
satisfy
![]() and
and
![]() , as indicated. Adding
, as indicated. Adding ![]() , it follows that
, it follows that
| (1) |
Let ![]() stand for a triangle side and
stand for a triangle side and ![]() for an angle, and let a set of
for an angle, and let a set of ![]() s and
s and ![]() s be concatenated such that adjacent letters
correspond to adjacent sides and angles in a triangle. Triangles are uniquely determined by specifying three sides
(SSS Theorem), two angles and a side (AAS Theorem), or two sides with an adjacent angle (SAS Theorem).
In each of these cases, the unknown three quantities (there are three sides and three angles total) can be uniquely
determined. Other combinations of sides and angles do not uniquely determine a triangle: three angles specify a
triangle only modulo a scale size (AAA Theorem), and one angle and two sides not containing it may specify one,
two, or no triangles (ASS Theorem).
s be concatenated such that adjacent letters
correspond to adjacent sides and angles in a triangle. Triangles are uniquely determined by specifying three sides
(SSS Theorem), two angles and a side (AAS Theorem), or two sides with an adjacent angle (SAS Theorem).
In each of these cases, the unknown three quantities (there are three sides and three angles total) can be uniquely
determined. Other combinations of sides and angles do not uniquely determine a triangle: three angles specify a
triangle only modulo a scale size (AAA Theorem), and one angle and two sides not containing it may specify one,
two, or no triangles (ASS Theorem).
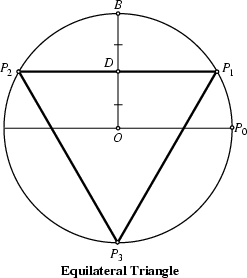
The Straightedge and Compass construction of the triangle can be accomplished as follows. In the above figure, take
![]() as a Radius and draw
as a Radius and draw ![]() . Then bisect
. Then bisect ![]() and construct
and construct ![]() . Extending
. Extending ![]() to
locate
to
locate ![]() then gives the Equilateral Triangle
then gives the Equilateral Triangle
![]() .
.
In Proposition IV.4 of the Elements, Euclid ![]() showed how to inscribe a Circle (the
Incircle) in a given triangle by locating the Center as the point of intersection of Angle
Bisectors. In Proposition IV.5, he showed how to circumscribe a Circle (the Circumcircle)
about a given triangle by locating the Center as the point of intersection of the perpendicular bisectors.
showed how to inscribe a Circle (the
Incircle) in a given triangle by locating the Center as the point of intersection of Angle
Bisectors. In Proposition IV.5, he showed how to circumscribe a Circle (the Circumcircle)
about a given triangle by locating the Center as the point of intersection of the perpendicular bisectors.
If the coordinates of the triangle Vertices are given by ![]() where
where ![]() 2, 3, then
the Area
2, 3, then
the Area ![]() is given by the Determinant
is given by the Determinant
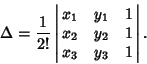 |
(2) |
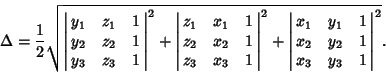 |
(3) |
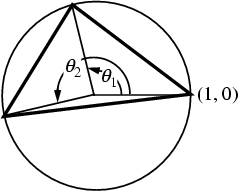
In the above figure, let the Circumcircle passing through a triangle's Vertices have
Radius ![]() , and denote the Central Angles from the first point to the second
, and denote the Central Angles from the first point to the second ![]() ,
and to the third point by
,
and to the third point by ![]() . Then the Area of the triangle is given by
. Then the Area of the triangle is given by
| (4) |
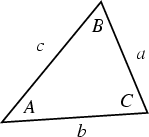
If a triangle has sides ![]() ,
, ![]() ,
, ![]() , call the angles opposite these sides
, call the angles opposite these sides ![]() ,
, ![]() , and
, and ![]() , respectively. Also
define the Semiperimeter
, respectively. Also
define the Semiperimeter ![]() as Half the Perimeter:
as Half the Perimeter:
| (5) |
| (6) |
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
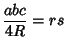 |
(12) | ||
| (13) | |||
| (14) |
| (15) | |||
| (16) | |||
| (17) |
| (18) |
The Angles of a triangle satisfy
| (19) |
| (20) |
Let a triangle have Angles ![]() ,
, ![]() , and
, and ![]() . Then
. Then
| (21) |
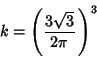 |
(22) |
| (23) |
Trigonometric Functions of half angles can be expressed in terms of the triangle sides:
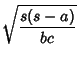 |
(24) | ||
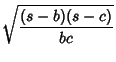 |
(25) | ||
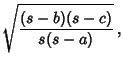 |
(26) |
The number of different triangles which have Integral sides and Perimeter ![]() is
is
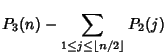 |
|||
![$\displaystyle \left[{n^2\over 12}\right]-\left\lfloor{n\over 4}\right\rfloor \left\lfloor{n+2\over 4}\right\rfloor$](t_1329.gif) |
|||
![$\displaystyle \left\{\begin{array}{ll} \left[{n^2\over 48}\right]& \mbox{for $n$\ even}\\ \left[{(n+3)^2\over 48}\right]& \mbox{for $n$\ odd,}\end{array}\right.$](t_1330.gif) |
(27) |
| (28) |
It is not known if a triangle with Integer sides, Medians, and Area exists (although there are incorrect Proofs of the impossibility in the literature). However, R. L. Rathbun, A. Kemnitz, and R. H. Buchholz have shown that there are infinitely many triangles with Rational sides (Heronian Triangles) with two Rational Medians (Guy 1994).
In the following paragraph, assume the specified sides and angles are adjacent to each other. Specifying three
Angles does not uniquely define a triangle, but any two triangles with the same Angles
are similar (the AAA Theorem). Specifying two Angles ![]() and
and ![]() and a side
and a side ![]() uniquely
determines a triangle with Area
uniquely
determines a triangle with Area
| (29) |
| (30) |
| (31) |
| (32) |
There are four Circles which are tangent to the sides of a triangle, one internal and the rest external. Their centers are the points of intersection of the Angle Bisectors of the triangle.
Any triangle can be positioned such that its shadow under an orthogonal projection is Equilateral.
See also AAA Theorem, AAS Theorem, Acute Triangle, Alcuin's Sequence, Altitude, Angle Bisector, Anticevian Triangle, Anticomplementary Triangle, Antipedal Triangle, ASS Theorem, Bell Triangle, Brianchon Point, Brocard Angle, Brocard Circle, Brocard Midpoint, Brocard Points, Butterfly Theorem, Centroid (Triangle), Ceva's Theorem, Cevian, Cevian Triangle, Chasles's Theorem, Circumcenter, Circumcircle, Circumradius, Contact Triangle, Crossed Ladders Problem, Crucial Point, D-Triangle, de Longchamps Point, Desargues' Theorem, Dissection, Elkies Point, Equal Detour Point, Equilateral Triangle, Euler Line, Euler's Triangle, Euler Triangle Formula, Excenter, Excentral Triangle, Excircle, Exeter Point, Exmedian, Exmedian Point, Exradius, Exterior Angle Theorem, Fagnano's Problem, Far-Out Point, Fermat Point, Fermat's Problem, Feuerbach Point, Feuerbach's Theorem, Fuhrmann Triangle, Gergonne Point, Grebe Point, Griffiths Points, Griffiths' Theorem, Harmonic Conjugate Points, Heilbronn Triangle Problem, Heron's Formula, Heronian Triangle, Hofstadter Triangle, Homothetic Triangles, Incenter, Incircle, Inradius, Isodynamic Points, Isogonal Conjugate, Isogonic Centers, Isoperimetric Point, Isosceles Triangle, Kabon Triangles, Kanizsa Triangle, Kiepert's Hyperbola, Kiepert's Parabola, Law of Cosines, Law of Sines, Law of Tangents, Leibniz Harmonic Triangle, Lemoine Circle, Lemoine Point, Line at Infinity, Malfatti Points, Medial Triangle, Median (Triangle), Median Triangle, Menelaus' Theorem, Mid-Arc Points, Mittenpunkt, Mollweide's Formulas, Morley Centers, Morley's Theorem, Nagel Point, Napoleon's Theorem, Napoleon Triangles, Newton's Formulas, Nine-Point Circle, Number Triangle, Obtuse Triangle, Orthic Triangle, Orthocenter, Orthologic, Paralogic Triangles, Pascal's Triangle, Pasch's Axiom, Pedal Triangle, Perpendicular Bisector, Perspective Triangles, Petersen-Shoute Theorem, Pivot Theorem, Power Point, Power (Triangle), Prime Triangle, Purser's Theorem, Quadrilateral, Rational Triangle, Routh's Theorem, SAS Theorem, Scalene Triangle, Schiffler Point, Schwarz Triangle, Schwarz's Triangle Problem, Seidel-Entringer-Arnold Triangle, Seydewitz's Theorem, Simson Line, Spieker Center, SSS Theorem, Steiner-Lehmus Theorem, Steiner Points, Stewart's Theorem, Symmedian Point, Tangential Triangle, Tangential Triangle Circumcenter, Tarry Point, Thomsen's Figure, Torricelli Point, Triangle Tiling, Triangle Transformation Principle, Yff Points, Yff Triangles
References
Abi-Khuzam, F. ``Proof of Yff's Conjecture on the Brocard Angle of a Triangle.'' Elem. Math. 29, 141-142, 1974.
Andrews, G. ``A Note on Partitions and Triangles with Integer Sides.'' Amer. Math. Monthly 86, 477, 1979.
Baker, M. ``A Collection of Formulæ for the Area of a Plane Triangle.'' Ann. Math. 1, 134-138, 1884.
Berkhan, G. and Meyer, W. F. ``Neuere Dreiecksgeometrie.'' In Encyklopaedie der Mathematischen Wissenschaften, Vol. 3AB 10
(Ed. F. Klein). Leipzig: Teubner, pp. 1173-1276, 1914.
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 123-124, 1987.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.
Davis, P. ``The Rise, Fall, and Possible Transfiguration of Triangle Geometry: A Mini-History.'' Amer. Math. Monthly 102,
204-214, 1995.
Eppstein, D. ``Triangles and Simplices.''
http://www.ics.uci.edu/~eppstein/junkyard/triangulation.html.
Feuerbach, K. W.
Eigenschaften einiger merkwürdingen Punkte des geradlinigen Dreiecks, und mehrerer durch die bestimmten Linien und Figuren.
Nürnberg, Germany, 1822.
Guy, R. K. ``Triangles with Integer Sides, Medians, and Area.'' §D21
in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 188-190, 1994.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 39-47, 1985.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, 1929.
Jordan, J. H.; Walch, R.; and Wisner, R. J. ``Triangles with Integer Sides.'' Amer. Math. Monthly 86, 686-689, 1979.
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Kimberling, C. ``Triangle Centers and Central Triangles.'' Congr. Numer. 129, 1-295, 1998.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 28, 1983.
Schroeder. Das Dreieck und seine Beruhungskreise.
Sloane, N. J. A. Sequence
A005044/M0146
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vandeghen, A. ``Some Remarks on the Isogonal and Cevian Transforms. Alignments of Remarkable Points of a Triangle.''
Amer. Math. Monthly 72, 1091-1094, 1965.
![]() Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
|
|
|
© 1996-9 Eric W. Weisstein