|
|
|
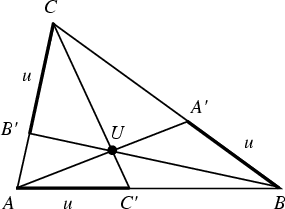
Let points ![]() ,
, ![]() , and
, and ![]() be marked off some fixed distance
be marked off some fixed distance ![]() along each of the sides
along each of the sides ![]() ,
, ![]() , and
, and ![]() .
Then the lines
.
Then the lines ![]() ,
, ![]() , and
, and ![]() concur in a point
concur in a point ![]() known as the first Yff point if
known as the first Yff point if
| (1) |
| (2) |
| (3) | |||
| (4) | |||
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Yff (1963) gives a number of other interesting properties. The line ![]() is Perpendicular to the line containing
the Incenter
is Perpendicular to the line containing
the Incenter ![]() and Circumcenter
and Circumcenter ![]() , and its length is given by
, and its length is given by
| (10) |
See also Brocard Points, Yff Triangles
References
Yff, P. ``An Analog of the Brocard Points.'' Amer. Math. Monthly 70, 495-501, 1963.
|
|
|
© 1996-9 Eric W. Weisstein