|
|
|
The Area of a Surface is the amount of material needed to ``cover'' it completely. The Area of a Triangle is
given by
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Calculus and, in particular, the Integral, are powerful tools for computing the Area between a curve
![]() and the x-Axis over an Interval
and the x-Axis over an Interval ![]() , giving
, giving
| (6) |
| (7) |
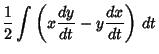 |
(8) | ||
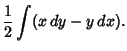 |
(9) |
For the Area of special surfaces or regions, see the entry for that region. The generalization of Area to 3-D is called Volume, and to higher Dimensions is called Content.
See also Arc Length, Area Element, Content, Surface Area, Volume
References
Gray, A. ``The Intuitive Idea of Area on a Surface.'' §13.2 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 259-260, 1993.
|
|
|
© 1996-9 Eric W. Weisstein