|
|
|
The term square is sometimes used to mean Square Number. When used in reference to a geometric figure, however, it means a convex Quadrilateral with four equal sides at Right Angles to each other, illustrated above.
The Perimeter of a square with side length ![]() is
is
| (1) |
| (2) |
| (3) | |||
| (4) | |||
| (5) |
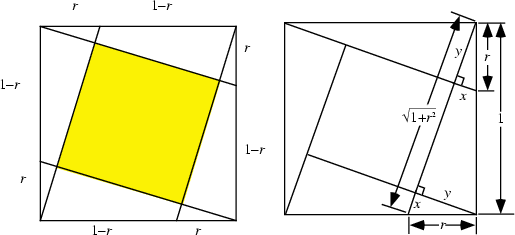
The Area of a square inscribed inside a Unit Square as shown in the above diagram can be found as follows. Label
![]() and
and ![]() as shown, then
as shown, then
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
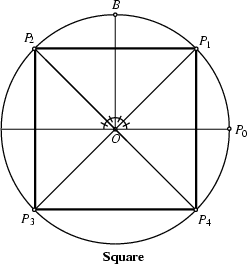
The Straightedge and Compass construction of the square is simple. Draw the line ![]() and construct a circle
having
and construct a circle
having ![]() as a radius. Then construct the perpendicular
as a radius. Then construct the perpendicular ![]() through
through ![]() . Bisect
. Bisect ![]() and
and ![]() to locate
to locate ![]() and
and
![]() , where
, where ![]() is opposite
is opposite ![]() . Similarly, construct
. Similarly, construct ![]() and
and ![]() on the other Semicircle. Connecting
on the other Semicircle. Connecting
![]() then gives a square.
then gives a square.
As shown by Schnirelmann, a square can be Inscribed in any closed convex planar curve (Steinhaus 1983). A square can also be Circumscribed about any closed curve (Steinhaus 1983).
An infinity of points in the interior of a square are known whose distances from three of the corners of a square are
Rational Numbers. Calling the distances ![]() ,
, ![]() , and
, and ![]() where
where ![]() is the side length of the
square, these solutions satisfy
is the side length of the
square, these solutions satisfy
| (13) |
| (14) |
See also Browkin's Theorem, Dissection, Douglas-Neumann Theorem, Finsler-Hadwiger Theorem, Lozenge, Perfect Square Dissection, Pythagoras's Constant, Pythagorean Square Puzzle, Rectangle, Square Cutting, Square Number, Square Packing, Square Quadrants, Unit Square, von Aubel's Theorem
References
Detemple, D. and Harold, S. ``A Round-Up of Square Problems.'' Math. Mag. 69, 15-27, 1996.
Dixon, R. Mathographics. New York: Dover, p. 16, 1991.
Eppstein, D. ``Rectilinear Geometry.''
http://www.ics.uci.edu/~eppstein/junkyard/rect.html.
Guy, R. K. ``Rational Distances from the Corners of a Square.'' §D19 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 181-185, 1994.
Steinhaus, H. Mathematical Snapshots, 3rd American ed. New York: Oxford University Press, p. 104, 1983.
|
|
|
© 1996-9 Eric W. Weisstein