|
|
|
A Square which can be Dissected into a number of smaller Squares with no two equal is called a Perfect Square Dissection (or a Squared Square). Square dissections in which the squares need not be different sizes are called Mrs. Perkins' Quilts. If no subset of the Squares forms a Rectangle, then the perfect square is called ``simple.'' Lusin claimed that perfect squares were impossible to construct, but this assertion was proved erroneous when a 55-Square perfect square was published by R. Sprague in 1939 (Wells 1991).
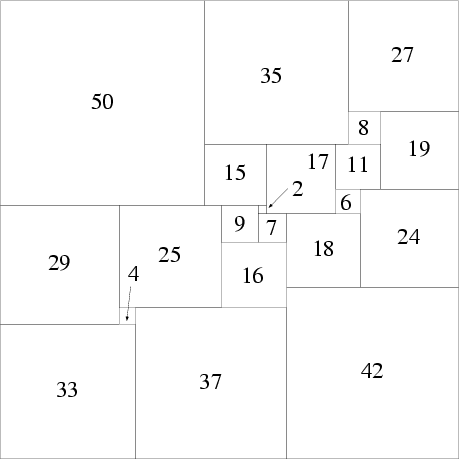
There is a unique simple perfect square of order 21 (the lowest possible order), discovered in 1978 by A. J. W. Duijvestijn (Bouwkamp and Duijvestijn 1992). It is composed of 21 squares with total side length 112, and is illustrated above. There is a simple notation (sometimes called Bouwkamp code) used to describe perfect squares. In this notation, brackets are used to group adjacent squares with flush tops, and then the groups are sequentially placed in the highest (and leftmost) possible slots. For example, the 21-square illustrated above is denoted [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].
The number of simple perfect squares of order ![]() for
for ![]() are 1, 8, 12, 26, 160, 441, ... (Sloane's A006983).
Duijvestijn's Table I gives a list of the 441 simple perfect squares of order 26, the smallest with side length 212 and the
largest with side length 825. Skinner (1993) gives the smallest possible side length (and smallest order for each) as 110
(22), 112 (21), 120 (24), 139 (22), 140 (23), ... for simple perfect squared squares, and 175 (24), 235 (25), 288 (26),
324 (27), 325 (27), ... for compound perfect squared squares.
are 1, 8, 12, 26, 160, 441, ... (Sloane's A006983).
Duijvestijn's Table I gives a list of the 441 simple perfect squares of order 26, the smallest with side length 212 and the
largest with side length 825. Skinner (1993) gives the smallest possible side length (and smallest order for each) as 110
(22), 112 (21), 120 (24), 139 (22), 140 (23), ... for simple perfect squared squares, and 175 (24), 235 (25), 288 (26),
324 (27), 325 (27), ... for compound perfect squared squares.
There are actually three simple perfect squares having side length 110. They are [60, 50], [23, 27], [24, 22, 14], [7, 16], [8, 6], [12, 15], [13], [2, 28], [26], [4, 21, 3], [18], [17] (order 22; discovered by A. J. W. Duijvestijn); [60, 50], [27, 23], [24, 22, 14], [4, 19], [8, 6], [3, 12, 16], [9], [2, 28], [26], [21], [1, 18], [17] (order 22; discovered by T. H. Willcocks); and [44, 29, 37], [21, 8], [13, 32], [28, 16], [15, 19], [12,4], [3, 1], [2, 14], [5], [10, 41], [38, 7], [31] (order 23; discovered by A. J. W. Duijvestijn).
D. Sleator has developed an efficient Algorithm for finding non-simple perfect squares using what he calls
rectangle and ``ell'' grow sequences. This algorithm finds a slew of compound perfect squares of orders 24-32. Weisstein
gives a partial list of known simple and compound perfect squares (where the number of simple perfect squares is exact for
orders less than 27) as well as Mathematica
![]() (Wolfram Research, Champaign, IL) algorithms for drawing them.
(Wolfram Research, Champaign, IL) algorithms for drawing them.
| Order | # Simple | # Compound |
| 21 | 1 | 0 |
| 22 | 8 | 0 |
| 23 | 12 | 0 |
| 24 | 26 | 1 |
| 25 | 160 | 1 |
| 26 | 441 | 2 |
| 27 | ? | 2 |
| 28 | ? | 4 |
| 29 | ? | 2 |
| 30 | ? | 3 |
| 31 | ? | 2 |
| 32 | ? | 2 |
| 38 | 1 | 0 |
| 69 | 1 | 0 |
See also Mrs. Perkins' Quilt
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 115-116, 1987.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York:
Dover, pp. 157-161, 1966.
Bouwkamp, C. J. and Duijvestijn, A. J. W. ``Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25.''
Eindhoven Univ. Technology, Dept. Math, Report 92-WSK-03, Nov. 1992.
Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. ``The Dissection of Rectangles into Squares.''
Duke Math. J. 7, 312-340, 1940.
Duijvestijn, A. J. W. ``A Simple Perfect Square of Lowest Order.'' J. Combin. Th. Ser. B 25, 240-243, 1978.
Duijvestijn, A. J. W. ``A Lowest Order Simple Perfect
Duijvestijn, A. J. W. ftp://ftp.cs.utwente.nl/pub/doc/dvs/TableI.
Gardner, M. ``Squaring the Square.'' Ch. 17 in
The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection.
New York: Simon and Schuster, 1961.
Gardner, M. Fractal Music, Hypercards, and More: Mathematical Recreations from Scientific American Magazine.
New York: W. H. Freeman, pp. 172-174, 1992.
Kraitchik, M. Mathematical Recreations. New York: W. W. Norton, p. 198, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 15 and 32-33, 1979.
Mauldin, R. D. (Ed.) The Scottish Book: Math at the Scottish Cafe Boston, MA: Birkhäuser, 1982.
Moron, Z. ``O rozk
Skinner, J. D. II. Squared Squares: Who's Who & What's What. Published by the author, 1993.
Sloane, N. J. A. Sequence
A006983/M4482
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in
Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Sprague, R. ``Beispiel einer Zerlegung des Quadrats in lauter verschiedene Quadrate.'' Math. Z. 45, 607-608, 1939.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 242, 1991.
![]() Squared Rectangle.'' J. Combin. Th. Ser. B 26, 372-374, 1979.
Squared Rectangle.'' J. Combin. Th. Ser. B 26, 372-374, 1979.
![]() adach prostokatów na kwadraty.'' Przeglad matematyczno-fizyczny 3, 152-153, 1925.
adach prostokatów na kwadraty.'' Przeglad matematyczno-fizyczny 3, 152-153, 1925.
![]() Weisstein, E. W. ``Perfect Squares.'' Mathematica notebook PerfectSquare.m.
Weisstein, E. W. ``Perfect Squares.'' Mathematica notebook PerfectSquare.m.
|
|
|
© 1996-9 Eric W. Weisstein