|
|
|
The radius of a Triangle's Circumcircle or of a Polyhedron's Circumsphere, denoted ![]() .
For a Triangle,
.
For a Triangle,
| (1) |
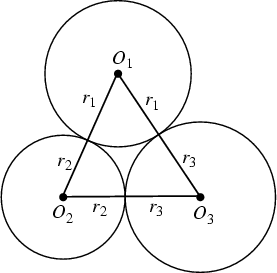
This equation can also be expressed in terms of the Radii of the three mutually tangent
Circles centered at the Triangle's Vertices. Relabeling the diagram for
the Soddy Circles with Vertices ![]() ,
, ![]() , and
, and ![]() and the radii
and the radii ![]() ,
, ![]() , and
, and
![]() , and using
, and using
| (2) | |||
| (3) | |||
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
For an Archimedean Solid, expressing the circumradius in terms of the Inradius ![]() and Midradius
and Midradius
![]() gives
gives
| (13) | |||
| (14) |
See also Carnot's Theorem, Circumcircle, Circumsphere
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, 1929.
Mackay, J. S. ``Historical Notes on a Geometrical Theorem and its Developments [18th Century].''
Proc. Edinburgh Math. Soc. 5, 62-78, 1886-1887.
|
|
|
© 1996-9 Eric W. Weisstein