|
|
|
The Radius of the Midsphere of a Polyhedron, also called the Interradius. For a Regular
Polyhedron with Schläfli Symbol ![]() , the Dual Polyhedron is
, the Dual Polyhedron is ![]() . Denote
the Inradius
. Denote
the Inradius ![]() , midradius
, midradius ![]() , and Circumradius
, and Circumradius ![]() , and let the side length be
, and let the side length be ![]() . Then
. Then
![$\displaystyle \left[{a \csc\left({\pi\over p}\right)}\right]^2+R^2=a^2+\rho^2$](m_1180.gif) |
(1) | ||
![$\displaystyle \left[{a\cot\left({\pi\over p}\right)}\right]^2+R^2.$](m_1182.gif) |
(2) |
| (3) | |||
| (4) | |||
| (5) |
| (6) |
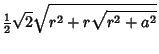 |
|||
| (7) |
References
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 126-127, 1989.