|
|
|
By the Duality Principle, for every Polyhedron, there exists another Polyhedron in which faces and Vertices occupy complementary locations. This Polyhedron is known as the dual, or Reciprocal. The dual polyhedron of a Platonic Solid or Archimedean Solid can be drawn by constructing Edges tangent to the Reciprocating Sphere (a.k.a. Midsphere and Intersphere) which are Perpendicular to the original Edges.
The dual of a general solid can be computed by connecting the midpoints of the sides surrounding each Vertex, and constructing the corresponding tangent Polygon. (The tangent polygon is the polygon which is tangent to the Circumcircle of the Polygon produced by connecting the Midpoint on the sides surrounding the given Vertex.) The process is illustrated below for the Platonic Solids. The Polyhedron Compounds consisting of a Polyhedron and its dual are generally very attractive, and are also illustrated below for the Platonic Solids.
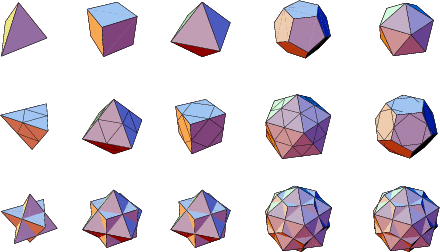
The Archimedean Solids and their duals are illustrated below.
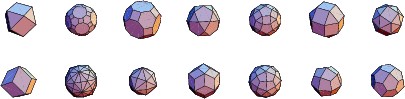
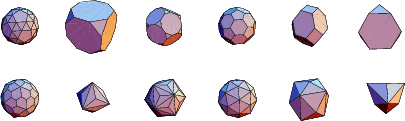
The following table gives a list of the duals of the Platonic Solids and Kepler-Poinsot Solids together with the names of the Polyhedron-dual Compounds.
See also Duality Principle, Polyhedron Compound, Reciprocating Sphere
References
Wenninger, M. Dual Models. Cambridge, England: Cambridge University Press, 1983.
![]() Weisstein, E. W. ``Polyhedron Duals.'' Mathematica notebook Duals.m.
Weisstein, E. W. ``Polyhedron Duals.'' Mathematica notebook Duals.m.
|
|
|
© 1996-9 Eric W. Weisstein