|
|
|
|
A Polyhedron Compound of a Dodecahedron and Icosahedron which is most easily constructed by adding 20
triangular Pyramids, constructed as above, to an Icosahedron. In the compound, the
Dodecahedron and Icosahedron are rotated ![]() radians with respect to each other, and the ratio of the
Icosahedron to Dodecahedron edges lengths are the Golden Ratio
radians with respect to each other, and the ratio of the
Icosahedron to Dodecahedron edges lengths are the Golden Ratio ![]() .
.
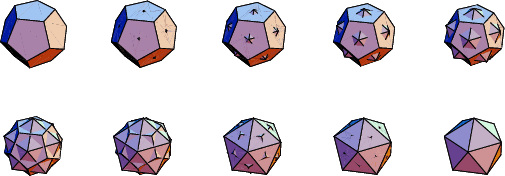
The above figure shows compounds composed of a Dodecahedron of unit edge length and Icosahedra
having edge lengths varying from ![]() (inscribed in the dodecahedron) to 2 (circumscribed about the dodecahedron).
(inscribed in the dodecahedron) to 2 (circumscribed about the dodecahedron).
The intersecting edges of the compound form the Diagonals of 30 Rhombuses comprising the Triacontahedron, which is the Dual Polyhedron of the Icosidodecahedron (Ball and Coxeter 1987). The dodecahedron-icosahedron is the first Stellation of the Icosidodecahedron.
See also Dodecahedron, Icosahedron, Icosidodecahedron, Polyhedron Compound
References
Cundy, H. and Rollett, A. Mathematical Models, 2nd ed. Stradbroke, England: Tarquin Pub., p. 131, 1989.
Wenninger, M. J. Polyhedron Models. Cambridge, England: Cambridge University Press, p. 76, 1989.