Octahedron

A Platonic Solid ($P_3$) with six Vertices, 12 Edges, and eight equivalent Equilateral Triangular faces ($8\{3\}$), given by the Schläfli Symbol $\{3,4\}$. It is also Uniform Polyhedron $U_5$ with the Wythoff Symbol $4\,\vert\,2\,3$. Its Dual Polyhedron is the Cube. Like the Cube, it has the $O_h$ Octahedral Group of symmetries. The octahedron can be Stellated to give the Stella Octangula.

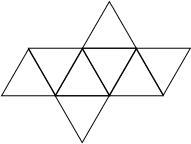
The solid bounded by the two Tetrahedra of the Stella Octangula (left figure) is an octahedron (right figure; Ball and Coxeter 1987).

In one orientation (left figure), the Vertices are given by $(\pm 1,0,0)$, $(0,\pm 1,0)$, $(0,0,\pm 1)$. In another orientation (right figure), the vertices are $(\pm 1, \pm 1, 0)$ and $(0,0,\pm\sqrt{2}\,)$. In the latter, the constituent Triangles are specified by

$$T_1 = \{(-1,-1,0), ( 1,-1,0), (0,0,\sqrt{2}\,)\}$$

$$T_2 = \{(-1,-1,0), ( 1,-1,0), (0,0,-\sqrt{2}\,)\}$$

$$T_3 = \{(-1, 1,0), ( 1, 1,0), (0,0,\sqrt{2}\,)\}$$

$$T_4 = \{(-1, 1,0), ( 1, 1,0), (0,0,-\sqrt{2}\,)\}$$

$$T_5 = \{( 1,-1,0), ( 1, 1,0), (0,0,\sqrt{2}\,)\}$$

$$T_6 = \{(-1,-1,0), (-1, 1,0), (0,0,\sqrt{2}\,)\}$$

$$T_7 = \{( 1,-1,0), ( 1, 1,0), (0,0,-\sqrt{2}\,)\}$$

$$T_8 = \{(-1,-1,0), (-1, 1,0), (0,0,-\sqrt{2}\,)\}.$$

The face planes are $\pm x\pm y\pm z=1$, so a solid octahedron is given by the equation

$$\vert x\vert+\vert y\vert+\vert z\vert\leq 1.$$ (1)

A plane Perpendicular to a $C_3$ axis of an octahedron cuts the solid in a regular Hexagonal Cross-Section (Holden 1991, pp. 22-23). Since there are four such axes, there are four possibly Hexagonal Cross-Sections. Faceted forms are the Cuboctatruncated Cuboctahedron and Tetrahemihexahedron.

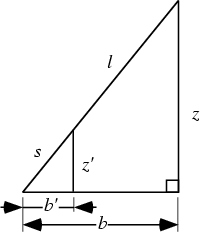
Let an octahedron be length $a$ on a side. The height of the top Vertex from the square plane is also the Circumradius

$$R=\sqrt{a^2-d^2}\,,$$ (2)

where

$$d={\textstyle{1\over 2}}\sqrt{2}\,a$$ (3)

is the diagonal length, so

$$R=\sqrt{a^2-{\textstyle{1\over 2}}a^2}={\textstyle{1\over 2}}\sqrt{2}\,a \approx 0.70710 a.$$ (4)

Now compute the Inradius.

$$\ell = {\textstyle{1\over 2}}\sqrt{3}\,a$$ (5)

$$b = {\textstyle{1\over 2}}a$$ (6)

$$s = {\textstyle{1\over 2}}a\tan 30^\circ = {a\over 2\sqrt{3}},$$ (7)

so

$${s\over\ell}={1\over 2\sqrt{3}}{2\over\sqrt{3}} = {\textstyle{1\over 3}}.$$ (8)

Now use similar Triangles to obtain

$$b' = {s\over\ell} b= {\textstyle{1\over 6}} a$$ (9)

$$z' = {s\over\ell} z={a\over 3\sqrt{2}}$$ (10)

$$x = b-b'={\textstyle{1\over 2}}a-{\textstyle{1\over 6}}a ={\textstyle{1\over 3}} a,$$ (11)

so the Inradius is

$$r=\sqrt{x^2+z'^2} = a\sqrt{{\textstyle{1\over 9}}+{\textstyl... ...r 18}}} ={\textstyle{1\over 6}} \sqrt{6}\,a \approx 0.40824 a.$$ (12)

The Interradius is

$$\rho={\textstyle{1\over 2}}a = 0.5a.$$ (13)

The Area of one face is the Area of an Equilateral Triangle

$$A={\textstyle{1\over 4}}\sqrt{3}\, a^2.$$ (14)

The volume is two times the volume of a square-base pyramid,

$$V=2({\textstyle{1\over 3}}a^2R)=2({\textstyle{1\over 3}})(a^... ...{1\over 2}}\sqrt{2}\, a)={\textstyle{1\over 3}}\sqrt{2}\, a^3.$$ (15)

The Dihedral Angle is

$$\alpha=\cos^{-1}({\textstyle{1\over 3}})\approx 70.528779^\circ.$$ (16)

See also Octahedral Graph, Octahedral Group, Octahedron 5-Compound, Stella Octangula, Truncated Octahedron

References

Davie, T. ``The Octahedron.'' http://www.dcs.st-and.ac.uk/~ad/mathrecs/polyhedra/octahedron.html.

Holden, A. Shapes, Space, and Symmetry. New York: Dover, 1991.