Semicircle

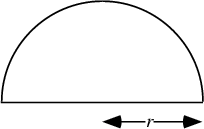
$\begin{figure}\begin{center}\BoxedEPSF{Semicircle.epsf scaled 1000}\end{center}\end{figure}$

Half a Circle. The Perimeter of the semicircle of Radius 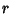is

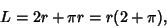$\begin{displaymath} L=2r+\pi r=r(2+\pi), \end{displaymath}$

(1)

and the Area is

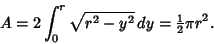$\begin{displaymath} A=2\int_0^r \sqrt{r^2-y^2}\,dy={\textstyle{1\over 2}}\pi r^2. \end{displaymath}$

(2)

The weighted mean of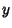

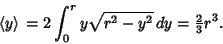$\begin{displaymath} \left\langle{y}\right\rangle{}=2\int_0^r y\sqrt{r^2-y^2}\,dy={\textstyle{2\over 3}}r^3. \end{displaymath}$

(3)

The Centroid is then given by

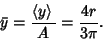$\begin{displaymath} \bar y={\left\langle{y}\right\rangle{}\over A}={4r\over 3\pi}. \end{displaymath}$

(4)

The semicircle is the Cross-Section of a Hemisphere for any Plane through the z-Axis.