|
|
|
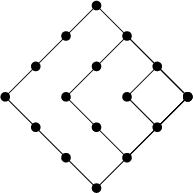
A Figurate Number of the form ![]() , where
, where ![]() is an Integer. A square number is also called a Perfect
Square. The first few square numbers are 1, 4, 9, 16, 25, 36, 49, ... (Sloane's A000290). The Generating Function giving
the square numbers is
is an Integer. A square number is also called a Perfect
Square. The first few square numbers are 1, 4, 9, 16, 25, 36, 49, ... (Sloane's A000290). The Generating Function giving
the square numbers is
| (1) |
The ![]() th nonsquare number
th nonsquare number ![]() is given by
is given by
| (2) |
The only numbers which are simultaneously square and Pyramidal (the Cannonball Problem)
are ![]() and
and ![]() , corresponding to
, corresponding to ![]() and
and ![]() (Dickson 1952, p. 25; Ball and Coxeter 1987,
p. 59; Ogilvy 1988), as conjectured by Lucas (1875, 1876) and proved by Watson (1918). The Cannonball Problem is
equivalent to solving the Diophantine Equation
(Dickson 1952, p. 25; Ball and Coxeter 1987,
p. 59; Ogilvy 1988), as conjectured by Lucas (1875, 1876) and proved by Watson (1918). The Cannonball Problem is
equivalent to solving the Diophantine Equation
| (3) |
The only numbers which are square and Tetrahedral are ![]() ,
, ![]() , and
, and ![]() (giving
(giving ![]() ,
, ![]() , and
, and ![]() ), as proved by Meyl (1878; cited in Dickson 1952, p. 25; Guy 1994, p. 147).
In general, proving that only certain numbers are simultaneously figurate in two different ways is far from elementary.
), as proved by Meyl (1878; cited in Dickson 1952, p. 25; Guy 1994, p. 147).
In general, proving that only certain numbers are simultaneously figurate in two different ways is far from elementary.
To find the possible last digits for a square number, write ![]() for the number written in decimal Notation as
for the number written in decimal Notation as
![]() (
(![]() ,
, ![]() , 1, ..., 9). Then
, 1, ..., 9). Then
| (4) |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 4 | 9 | _6 | _5 | _6 | _9 | _4 | _1 |
We can similarly examine the allowable last two digits by writing ![]() as
as
| (5) |
| (6) |
| c | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 01 | 21 | 41 | 61 | 81 | _01 | _21 | _41 | _61 | _81 |
| 4 | 16 | 96 | _76 | _56 | _36 | _16 | _96 | _76 | _56 | _36 |
| 5 | 25 | _25 | _25 | _25 | _25 | _25 | _25 | _25 | _25 | _25 |
| 6 | 36 | _56 | _76 | _96 | _16 | _36 | _56 | _76 | _96 | _16 |
| 9 | 81 | _61 | _41 | _21 | _01 | _81 | _61 | _41 | _21 | _01 |
The only possibilities are 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, and 96, which
can be summarized succinctly as 00, ![]() ,
, ![]() , 25,
, 25, ![]() , and
, and ![]() , where
, where ![]() stands for an Even Number and
stands for an Even Number and ![]() for an
Odd Number. Additionally, unless the sum of the digits of a number is 1, 4, 7, or 9, it cannot be a square number.
for an
Odd Number. Additionally, unless the sum of the digits of a number is 1, 4, 7, or 9, it cannot be a square number.
The following table gives the possible residues mod ![]() for square numbers for
for square numbers for ![]() to 20. The quantity
to 20. The quantity ![]() gives the
number of distinct residues for a given
gives the
number of distinct residues for a given ![]() .
.
|
|
||
| 2 | 2 | 0, 1 |
| 3 | 2 | 0, 1 |
| 4 | 2 | 0, 1 |
| 5 | 3 | 0, 1, 4 |
| 6 | 4 | 0, 1, 3, 4 |
| 7 | 4 | 0, 1, 2, 4 |
| 8 | 3 | 0, 1, 4 |
| 9 | 4 | 0, 1, 4, 7 |
| 10 | 6 | 0, 1, 4, 5, 6, 9 |
| 11 | 6 | 0, 1, 3, 4, 5, 9 |
| 12 | 4 | 0, 1, 4, 9 |
| 13 | 7 | 0, 1, 3, 4, 9, 10, 12 |
| 14 | 8 | 0, 1, 2, 4, 7, 8, 9, 11 |
| 15 | 6 | 0, 1, 4, 6, 9, 10 |
| 16 | 4 | 0, 1, 4, 9 |
| 17 | 9 | 0, 1, 2, 4, 8, 9, 13, 15, 16 |
| 18 | 8 | 0, 1, 4, 7, 9, 10, 13, 16 |
| 19 | 10 | 0, 1, 4, 5, 6, 7, 9, 11, 16, 17 |
| 20 | 6 | 0, 1, 4, 5, 9, 16 |
In general, the Odd squares are congruent to 1 (mod 8) (Conway and Guy 1996). Stangl (1996) gives an explicit formula by
which the number of squares ![]() in
in ![]() (i.e., mod
(i.e., mod ![]() ) can be calculated. Let
) can be calculated. Let ![]() be an Odd Prime. Then
be an Odd Prime. Then
![]() is the Multiplicative Function given by
is the Multiplicative Function given by
| (7) | |||
| (8) | |||
| (9) | |||
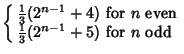 |
(10) | ||
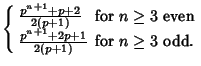 |
(11) |
| (12) |
For a perfect square ![]() ,
, ![]() or 1 for all Odd Primes
or 1 for all Odd Primes ![]() where
where ![]() is the Legendre Symbol.
A number
is the Legendre Symbol.
A number ![]() which is not a perfect square but which satisfies this relationship is called a Pseudosquare.
which is not a perfect square but which satisfies this relationship is called a Pseudosquare.
The minimum number of squares needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 1, 2, 3, 4, 2, 1, 2, ...
(Sloane's A002828), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of squares are 1, 1, 1, 2,
2, 2, 2, 3, 4, 4, ... (Sloane's A001156). A brute-force algorithm for enumerating the square permutations of ![]() is repeated
application of the Greedy Algorithm. However, this approach rapidly becomes impractical since the number of representations
grows extremely rapidly with
is repeated
application of the Greedy Algorithm. However, this approach rapidly becomes impractical since the number of representations
grows extremely rapidly with ![]() , as shown in the following table.
, as shown in the following table.
| Square Partitions | |
| 10 | 4 |
| 50 | 104 |
| 100 | 1116 |
| 150 | 6521 |
| 200 | 27482 |
Every Positive integer is expressible as a Sum of (at most) ![]() square numbers (Waring's Problem).
(Actually, the basis set is
square numbers (Waring's Problem).
(Actually, the basis set is
![]() , so 49 need never be used.) Furthermore, an
infinite number of
, so 49 need never be used.) Furthermore, an
infinite number of ![]() require four squares to represent them, so the related quantity
require four squares to represent them, so the related quantity ![]() (the least Integer
(the least Integer ![]() such that every Positive Integer beyond a certain point requires
such that every Positive Integer beyond a certain point requires ![]() squares) is given by
squares) is given by ![]() .
.
Numbers expressible as the sum of two squares are those whose Prime Factors are of the form
![]() taken to an Even Power. Numbers expressible as the sum of three squares are those not of the form
taken to an Even Power. Numbers expressible as the sum of three squares are those not of the form ![]() for
for ![]() . The following table gives the first few numbers which require
. The following table gives the first few numbers which require ![]() , 2, 3, and 4 squares to represent them as a
sum.
, 2, 3, and 4 squares to represent them as a
sum.
| Sloane | Numbers | |
| 1 | Sloane's A000290 | 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
| 2 | Sloane's A000415 | 2, 5, 8, 10, 13, 17, 18, 20, 26, 29, ... |
| 3 | Sloane's A000419 | 3, 6, 11, 12, 14, 19, 21, 22, 24, 27, ... |
| 4 | Sloane's A004215 | 7, 15, 23, 28, 31, 39, 47, 55, 60, 63, ... |
The Fermat 4n+1 Theorem guarantees that every Prime of the form ![]() is a sum of two Square
Numbers in only one way.
is a sum of two Square
Numbers in only one way.
There are only 31 numbers which cannot be expressed as the sum of distinct squares: 2, 3, 6, 7, 8, 11, 12, 15, 18, 19,
22, 23, 24, 27, 28, 31, 32, 33, 43, 44, 47, 48, 60, 67, 72, 76, 92, 96, 108, 112, 128 (Sloane's A001422; Guy 1994). All numbers
![]() can be expressed as the sum of at most five distinct squares, and only
can be expressed as the sum of at most five distinct squares, and only
| (13) |
| (14) |
| (15) |
| Sloane | Numbers | ||
| 1 | 1 | Sloane's A000290 | 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, ... |
| 2 | 1 | Sloane's A025284 | 2, 5, 8, 10, 13, 17, 18, 20, 25, 26, 29, 32, ... |
| 2 | 2 | Sloane's A025285 | 50, 65, 85, 125, 130, 145, 170, 185, 200, ... |
| 3 | 1 | Sloane's A025321 | 3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22, 24, ... |
| 3 | 2 | Sloane's A025322 | 27, 33, 38, 41, 51, 57, 59, 62, 69, 74, 75, ... |
| 3 | 3 | Sloane's A025323 | 54, 66, 81, 86, 89, 99, 101, 110, 114, 126, ... |
| 3 | 4 | Sloane's A025324 | 129, 134, 146, 153, 161, 171, 189, 198, ... |
| 4 | 1 | Sloane's A025357 | 4, 7, 10, 12, 13, 15, 16, 18, 19, 20, 21, 22, ... |
| 4 | 2 | Sloane's A025358 | 31, 34, 36, 37, 39, 43, 45, 47, 49, 50, 54, ... |
| 4 | 3 | Sloane's A025359 | 28, 42, 55, 60, 66, 67, 73, 75, 78, 85, 95, 99, ... |
| 4 | 4 | Sloane's A025360 | 52, 58, 63, 70, 76, 84, 87, 91, 93, 97, 98, 103, ... |
The number of Integers ![]() which are squares or sums of two squares is
which are squares or sums of two squares is
| (16) |
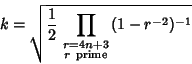 |
(17) |
| (18) | |||
| (19) | |||
| (20) |
| (21) | |||
| (22) | |||
| (23) |
Catalan's Conjecture states that 8 and 9 (![]() and
and ![]() ) are the only consecutive Powers (excluding 0
and 1), i.e., the only solution to Catalan's Diophantine Problem. This Conjecture has not yet been proved or
refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the Conjecture not
hold. It is also known that 8 and 9 are the only consecutive Cubic and square numbers (in either
order).
) are the only consecutive Powers (excluding 0
and 1), i.e., the only solution to Catalan's Diophantine Problem. This Conjecture has not yet been proved or
refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the Conjecture not
hold. It is also known that 8 and 9 are the only consecutive Cubic and square numbers (in either
order).
A square number can be the concatenation of two squares, as in the case ![]() and
and ![]() giving
giving ![]() .
.
It is conjectured that, other than ![]() ,
,
![]() and
and
![]() , there are only a Finite
number of squares
, there are only a Finite
number of squares ![]() having exactly two distinct Nonzero Digits (Guy 1994, p. 262). The first
few such
having exactly two distinct Nonzero Digits (Guy 1994, p. 262). The first
few such ![]() are 4, 5, 6, 7, 8, 9, 11, 12, 15, 21, ... (Sloane's A016070), corresponding to
are 4, 5, 6, 7, 8, 9, 11, 12, 15, 21, ... (Sloane's A016070), corresponding to ![]() of 16, 25, 36, 49, 64,
81, 121, ... (Sloane's A018884).
of 16, 25, 36, 49, 64,
81, 121, ... (Sloane's A018884).
The following table gives the first few numbers which, when squared, give numbers composed of only certain digits. The only known square number composed only of the digits 7, 8, and 9 is 9. Vardi (1991) considers numbers composed only of the square digits: 1, 4, and 9.
| Digits | Sloane | |
| 1, 2, 3 | Sloane's A030175 | 1, 11, 111, 36361, 363639, ...Sloane's A |
| Sloane's A030174 | 1, 121, 12321, 1322122321, ...Sloane's A | |
| 1, 4, 6 | Sloane's A027677 | 1, 2, 4, 8, 12, 21, 38, 108, ...Sloane's A |
| Sloane's A027676 | 1, 4, 16, 64, 144, 441, 1444, ...Sloane's A | |
| 1, 4, 9 | Sloane's A027675 | 1, 2, 3, 7, 12, 21, 38, 107, ...Sloane's A |
| Sloane's A006716 | 1, 4, 9, 49, 144, 441, 1444, 11449, ...Sloane's A | |
| 2, 4, 8 | Sloane's A027679 | 2, 22, 168, 478, 2878, 210912978, ...Sloane's A |
| Sloane's A027678 | 4, 484, 28224, 228484, 8282884, ...Sloane's A | |
| 4, 5, 6 | Sloane's A030177 | 2, 8, 216, 238, 258, 738, 6742, ...Sloane's A |
| Sloane's A030176 | 4, 64, 46656, 56644, 66564, ... |
Brown Numbers are pairs ![]() of Integers satisfying the condition of Brocard's Problem,
i.e., such that
of Integers satisfying the condition of Brocard's Problem,
i.e., such that
| (24) |
Either ![]() or
or ![]() has a solution in Positive Integers Iff, for some
has a solution in Positive Integers Iff, for some ![]() ,
,
![]() , where
, where ![]() is a Fibonacci Number and
is a Fibonacci Number and ![]() is a Lucas Number (Honsberger 1985, pp. 114-118).
is a Lucas Number (Honsberger 1985, pp. 114-118).
The smallest and largest square numbers containing the digits 1 to 9 are
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
Madachy (1979, p. 165) also considers number which are equal to the sum of the squares of their two ``halves'' such as
| (32) | |||
| (33) | |||
| (34) | |||
| (35) |
in addition to a number of others.
See also Antisquare Number, Biquadratic Number, Brocard's Problem, Brown Numbers, Cannonball Problem, Catalan's Conjecture, Centered Square Number, Clark's Triangle, Cubic Number, Diophantine Equation, Fermat 4n+1 Theorem, Greedy Algorithm, Gross, Lagrange's Four-Square Theorem, Landau-Ramanujan Constant, Pseudosquare, Pyramidal Number, r(n), Squarefree, Square Triangular Number, Waring's Problem
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Bohman, J.; Fröberg, C.-E.; and Riesel, H. ``Partitions in Squares.'' BIT 19, 297-301, 1979.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-32, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1952.
Grosswald, E. Representations of Integers as Sums of Squares. New York: Springer-Verlag, 1985.
Guy, R. K. ``Sums of Squares'' and ``Squares with Just Two Different Decimal Digits.'' §C20 and F24 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138 and 262, 1994.
Honsberger, R. ``A Second Look at the Fibonacci and Lucas Numbers.'' Ch. 8 in
Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Lucas, É. Question 1180. Nouv. Ann. Math. Ser. 2 14, 336, 1875.
Lucas, É. Solution de Question 1180. Nouv. Ann. Math. Ser. 2 15, 429-432, 1876.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 159 and 165, 1979.
Meyl, A.-J.-J. Solution de Question 1194. Nouv. Ann. Math. 17, 464-467, 1878.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, pp. 77 and 152, 1988.
Pappas, T. ``Triangular, Square & Pentagonal Numbers.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Pietenpol, J. L. ``Square Triangular Numbers.'' Amer. Math. Monthly 69, 168-169, 1962.
Robertson, J. P. ``Magic Squares of Squares.'' Math. Mag. 69, 289-293, 1996.
Stangl, W. D. ``Counting Squares in
Taussky-Todd, O. ``Sums of Squares.'' Amer. Math. Monthly 77, 805-830, 1970.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 20 and 234-237, 1991.
Watson, G. N. ``The Problem of the Square Pyramid.'' Messenger. Math. 48, 1-22, 1918.
![]() .'' Math. Mag. 69, 285-289, 1996.
.'' Math. Mag. 69, 285-289, 1996.
|
|
|
© 1996-9 Eric W. Weisstein