|
|
|
A Pythagorean triple is a Triple of Positive Integers ![]() ,
, ![]() , and
, and ![]() such that a Right
Triangle exists with legs
such that a Right
Triangle exists with legs ![]() and Hypotenuse
and Hypotenuse ![]() . By the Pythagorean Theorem, this is equivalent to finding
Positive Integers
. By the Pythagorean Theorem, this is equivalent to finding
Positive Integers ![]() ,
, ![]() , and
, and ![]() satisfying
satisfying
| (1) |
It is usual to consider only ``reduced'' (or ``primitive'') solutions in which ![]() and
and ![]() are Relatively Prime, since
other solutions can be generated trivially from the primitive ones. For primitive solutions, one of
are Relatively Prime, since
other solutions can be generated trivially from the primitive ones. For primitive solutions, one of ![]() or
or ![]() must be
Even, and the other Odd (Shanks 1993, p. 141), with
must be
Even, and the other Odd (Shanks 1993, p. 141), with ![]() always Odd. In addition, in every Pythagorean triple,
one side is always Divisible by 3 and one by 5.
always Odd. In addition, in every Pythagorean triple,
one side is always Divisible by 3 and one by 5.
Given a primitive triple ![]() , three new primitive triples are obtained from
, three new primitive triples are obtained from
| (2) | |||
| (3) | |||
| (4) |
![$\displaystyle \left[\begin{array}{ccc}1 & 2 & 2\\ -2 & -1 & -2\\ 2 & 2 & 3\end{array}\right]$](p3_1359.gif) |
(5) | ||
![$\displaystyle \left[\begin{array}{ccc}1 & 2 & 2\\ 2 & 1 & 2\\ 2 & 2 & 3\end{array}\right]$](p3_1361.gif) |
(6) | ||
![$\displaystyle \left[\begin{array}{ccc}-1 & -2 & -2\\ 2 & 1 & 2\\ 2 & 2 & 3\end{array}\right].$](p3_1363.gif) |
(7) |
| (8) |
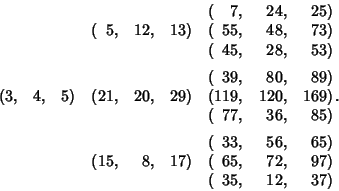 |
(9) |
For any Pythagorean triple, the Product of the two nonhypotenuse Legs (i.e., the two smaller
numbers) is always Divisible by 12, and the Product of all three sides is Divisible by 60. It is not
known if there are two distinct triples having the same Product. The existence of two such triples corresponds to a
Nonzero solution to the Diophantine Equation
| (10) |
Pythagoras ![]() and the Babylonians gave a formula for generating (not necessarily
primitive) triples:
and the Babylonians gave a formula for generating (not necessarily
primitive) triples:
| (11) |
| (12) |
| (13) |
| (14) |
For a Pythagorean triple (![]() ,
, ![]() ,
, ![]() ),
),
| (15) |
| (16) | |||
| (17) | |||
| (18) |
The Area of a Triangle corresponding to the Pythagorean triple
![]() is
is
| (19) |
To find the number ![]() of possible primitive Triangles which may have a Leg (other than the
Hypotenuse) of length
of possible primitive Triangles which may have a Leg (other than the
Hypotenuse) of length ![]() , factor
, factor ![]() into the form
into the form
| (20) |
| (21) |
| (22) |
![\begin{displaymath}
L(s)=\cases{
{\textstyle{1\over 2}}[(2a_1+1)(2a_2+1)\cdots(...
...cdots(2a_n+1)-1]\hfil\cr
\quad {\rm for\ }a_0\geq 2\hfill\cr}
\end{displaymath}](p3_1394.gif) |
(23) |
(Beiler 1966, p. 116). The first few numbers for ![]() , 2, ... are 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, ...
(Sloane's A046079).
, 2, ... are 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 4, 1, ...
(Sloane's A046079).
To find the number of ways ![]() in which a number
in which a number ![]() can be the Hypotenuse of a primitive Right
Triangle, write its factorization as
can be the Hypotenuse of a primitive Right
Triangle, write its factorization as
| (24) |
| (25) |
| (26) |
Therefore, the total number of ways in which ![]() may be either a Leg or Hypotenuse of a Right Triangle is
given by
may be either a Leg or Hypotenuse of a Right Triangle is
given by
| (27) |
There are 50 Pythagorean triples with Hypotenuse less than 100, the first few of which, sorted by increasing ![]() , are
, are
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , ... (Sloane's
A046083,
A046084,
and A046085).
Of these, only 16 are primitive triplets with Hypotenuse less than 100:
, ... (Sloane's
A046083,
A046084,
and A046085).
Of these, only 16 are primitive triplets with Hypotenuse less than 100: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (Sloane's
A046086,
A046087,
and A046088).
Of these 16 primitive triplets, seven are twin triplets (defined as triplets for which two members are consecutive integers).
The first few twin triplets, sorted by increasing
(Sloane's
A046086,
A046087,
and A046088).
Of these 16 primitive triplets, seven are twin triplets (defined as triplets for which two members are consecutive integers).
The first few twin triplets, sorted by increasing ![]() , are
, are
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
....
,
....
Let the number of triples with Hypotenuse less than ![]() be denoted
be denoted ![]() , and the number of twin triplets with
Hypotenuse less than
, and the number of twin triplets with
Hypotenuse less than ![]() be denoted
be denoted ![]() . Then, as the following table suggests and Lehmer (1900) proved, the
number of primitive solutions with Hypotenuse less than
. Then, as the following table suggests and Lehmer (1900) proved, the
number of primitive solutions with Hypotenuse less than ![]() satisfies
satisfies
| (28) |
| 100 | 16 | 0.1600 | 7 |
| 500 | 80 | 0.1600 | 17 |
| 1000 | 158 | 0.1580 | 24 |
| 2000 | 319 | 0.1595 | 34 |
| 3000 | 477 | 0.1590 | 41 |
| 4000 | 639 | 0.1598 | 47 |
| 5000 | 792 | 0.1584 | 52 |
| 10000 | 1593 | 0.1593 | 74 |
Considering twin triplets in which the Legs are consecutive, a closed form is available for the ![]() th such pair.
Consider the general reduced solution
th such pair.
Consider the general reduced solution
![]() , then the requirement that the Legs be
consecutive integers is
, then the requirement that the Legs be
consecutive integers is
| (29) |
| (30) |
| (31) | |||
| (32) |
| (33) |
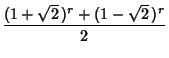 |
(34) | ||
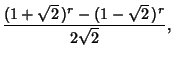 |
(35) |
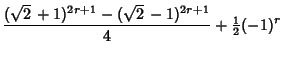 |
(36) | ||
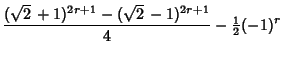 |
(37) | ||
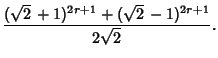 |
(38) |
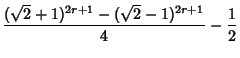 |
(39) | ||
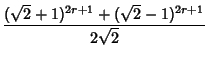 |
(40) |
| (41) |
| (42) |
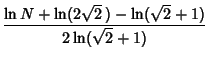 |
|||
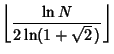 |
(43) | ||
| (44) |
Leg-Hypotenuse twin triples
![]() occur whenever
occur whenever
| (45) |
| (46) |
| (47) |
The total number of twin triples ![]() less than
less than ![]() is therefore approximately given by
is therefore approximately given by
| (48) | |||
| (49) |
There is a general method for obtaining triplets of Pythagorean triangles with equal Areas. Take the three
sets of generators as
| (50) | |||
| (51) |
| (52) | |||
| (53) |
| (54) | |||
| (55) |
| (56) |
One can also find quartets of Right Triangles with the same Area. The Quartet having smallest known area is (111, 6160, 6161), (231, 2960, 2969), (518, 1320, 1418), (280, 2442, 2458), with Area 341,880 (Beiler 1966, p. 127). Guy (1994) gives additional information.
It is also possible to find sets of three and four Pythagorean triplets having the same Perimeter (Beiler 1966,
pp. 131-132). Lehmer (1900) showed that the number of primitive triples ![]() with Perimeter less than
with Perimeter less than ![]() is
is
| (57) |
In 1643, Fermat ![]() challenged Mersenne to find a Pythagorean triplet whose Hypotenuse and Sum of
the Legs were Squares. Fermat
challenged Mersenne to find a Pythagorean triplet whose Hypotenuse and Sum of
the Legs were Squares. Fermat ![]() found the smallest such solution:
found the smallest such solution:
| (58) | |||
| (59) | |||
| (60) |
| (61) | |||
| (62) |
A related problem is to determine if a specified Integer ![]() can be the Area of a Right Triangle
with rational sides. 1, 2, 3, and 4 are not the Areas of any Rational-sided
Right Triangles, but 5 is (3/2, 20/3, 41/6), as is 6 (3, 4, 5). The solution to the problem
involves the Elliptic Curve
can be the Area of a Right Triangle
with rational sides. 1, 2, 3, and 4 are not the Areas of any Rational-sided
Right Triangles, but 5 is (3/2, 20/3, 41/6), as is 6 (3, 4, 5). The solution to the problem
involves the Elliptic Curve
| (63) |
| (64) | |||
| (65) |
See also Heronian Triangle, Pythagorean Quadruple, Right Triangle
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 57-59, 1987.
Beiler, A H. ``The Eternal Triangle.'' Ch. 14 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains.
New York: Dover, 1966.
Cipra, B. ``A Proof to Please Pythagoras.'' Science 271, 1669, 1996.
Courant, R. and Robbins, H. ``Pythagorean Numbers and Fermat's Last Theorem.'' §2.3 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 40-42, 1996.
Dickson, L. E. ``Rational Right Triangles.'' Ch. 4 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis.
New York: Chelsea, pp. 165-190, 1952.
Dixon, R. Mathographics. New York: Dover, p. 94, 1991.
Garfunkel, J. Pi Mu Epsilon J., p. 31, 1981.
Guy, R. K. ``Triangles with Integer Sides, Medians, and Area.''
§D21 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 188-190, 1994.
Hindin, H. ``Stars, Hexes, Triangular Numbers, and Pythagorean Triples.'' J. Recr. Math. 16, 191-193, 1983-1984.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., p. 47, 1985.
Koblitz, N. Introduction to Elliptic Curves and Modular Forms, 2nd ed. New York: Springer-Verlag, pp. 1-50, 1993.
Kraitchik, M. Mathematical Recreations. New York: W. W. Norton, pp. 95-104, 1942.
Kramer, K. and Tunnell, J. ``Elliptic Curves and Local Epsilon Factors.'' Comp. Math. 46, 307-352, 1982.
Lehmer, D. N. ``Asymptotic Evaluation of Certain Totient Sums.'' Amer. J. Math. 22, 294-335, 1900.
Roberts, J. Elementary Number Theory: A Problem Oriented Approach. Cambridge, MA: MIT Press, 1977.
Robertson, J. P. ``Magic Squares of Squares.'' Math. Mag. 69, 289-293, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 121 and 141, 1993.
Sloane, N. J. A. SequencesA002144/M3823, A005408/M2400, A006278, A006593/M2499, A020882, A024361, A046079, A046080,
A046081, A046083, A046084, A046085, A046086, A046087, A046089, A046090, A046091, A046092, and
A046093 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html..
Taussky-Todd, O. ``The Many Aspects of the Pythagorean Triangles.'' Linear Algebra and Appl. 43, 285-295, 1982.
|
|
|
© 1996-9 Eric W. Weisstein