|
|
|
An equation in which only Integer solutions are allowed. Hilbert's 10th Problem
asked if a technique for solving a general Diophantine existed. A general method exists for the solution of first degree
Diophantine equations. However, the impossibility of obtaining a general solution was proven by Julia Robinson and Martin
Davis in 1970, following proof of the result that the equation ![]() (where
(where ![]() is a Fibonacci Number) is
Diophantine by Yuri Matijasevic (Matijasevic 1970, Davis 1973, Davis and Hersh 1973, Matijasevic 1993).
is a Fibonacci Number) is
Diophantine by Yuri Matijasevic (Matijasevic 1970, Davis 1973, Davis and Hersh 1973, Matijasevic 1993).
No general method is known for solving quadratic or higher Diophantine equations. Jones and Matijasevic (1982) proved that no Algorithms can exist to determine if an arbitrary Diophantine equation in nine variables has solutions. Ogilvy and Anderson (1988) give a number of Diophantine equations with known and unknown solutions.
D. Wilson has compiled a list of the smallest ![]() th Powers which are the sums of
th Powers which are the sums of ![]() distinct
smaller
distinct
smaller ![]() th Powers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(Sloane's A030052):
th Powers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(Sloane's A030052):
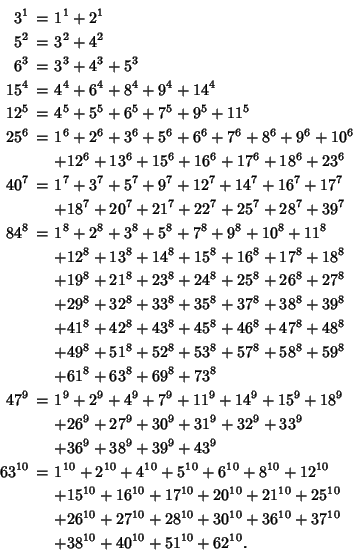
See also abc Conjecture, Archimedes' Cattle Problem, Bachet Equation, Brahmagupta's Problem, Cannonball Problem, Catalan's Problem, Diophantine Equation--Linear, Diophantine Equation--Quadratic, Diophantine Equation--Cubic, Diophantine Equation--Quartic, Diophantine Equation--5th Powers, Diophantine Equation--6th Powers, Diophantine Equation--7th Powers, Diophantine Equation--8th Powers, Diophantine Equation--9th Powers, Diophantine Equation--10th Powers, Diophantine Equation nth Powers, Diophantus Property, Euler Brick, Euler Quartic Conjecture, Fermat's Last Theorem, Fermat Sum Theorem, Genus Theorem, Hurwitz Equation, Markov Number, Monkey and Coconut Problem, Multigrade Equation, p-adic Number, Pell Equation, Pythagorean Quadruple, Pythagorean Triple
References
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Carmichael, R. D. The Theory of Numbers, and Diophantine Analysis. New York: Dover, 1959.
Chen, S. ``Equal Sums of Like Powers: On the Integer Solution of the Diophantine System.''
http://www.nease.net/~chin/eslp/.
Chen, S. ``References.''
http://www.nease.net/~chin/eslp/referenc.htm.
Davis, M. ``Hilbert's Tenth Problem is Unsolvable.'' Amer. Math. Monthly 80, 233-269, 1973.
Davis, M. and Hersh, R. ``Hilbert's 10th Problem.'' Sci. Amer., pp. 84-91, Nov. 1973.
Dörrie, H. ``The Fermat-Gauss Impossibility Theorem.'' §21 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 96-104, 1965.
Guy, R. K. ``Diophantine Equations.'' Ch. D in Unsolved Problems in Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 139-198, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hunter, J. A. H. and Madachy, J. S. ``Diophantos and All That.'' Ch. 6 in Mathematical Diversions. New York:
Dover, pp. 52-64, 1975.
Ireland, K. and Rosen, M. ``Diophantine Equations.'' Ch. 17 in
A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 269-296, 1990.
Jones, J. P. and Matijasevic, Yu. V. ``Exponential Diophantine Representation of Recursively Enumerable Sets.''
Proceedings of the Herbrand Symposium, Marseilles, 1981. Amsterdam, Netherlands: North-Holland, pp. 159-177, 1982.
Lang, S. Introduction to Diophantine Approximations, 2nd ed. New York: Springer-Verlag, 1995.
Matijasevic, Yu. V. ``Solution of the Tenth Problem of Hilbert.'' Mat. Lapok 21, 83-87, 1970.
Matijasevic, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993.
Mordell, L. J. Diophantine Equations. New York: Academic Press, 1969.
Nagel, T. Introduction to Number Theory. New York: Wiley, 1951.
Ogilvy, C. S. and Anderson, J. T. ``Diophantine Equations.'' Ch. 6 in Excursions in Number Theory. New York:
Dover, pp. 65-83, 1988.
Sloane, N. J. A. Sequence
A030052
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
![]() Diophantine Equations
Diophantine Equations
|
|
|
© 1996-9 Eric W. Weisstein