The 2-1 equation
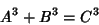 |
(1) |
is a case of Fermat's Last Theorem with 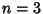 . In fact, this particular case was known not to have any solutions
long before the general validity of Fermat's Last Theorem was established. The 2-2 equation
. In fact, this particular case was known not to have any solutions
long before the general validity of Fermat's Last Theorem was established. The 2-2 equation
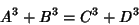 |
(2) |
has a known parametric solution (Dickson 1966, pp. 550-554; Guy 1994, p. 140), and 10 solutions with sum 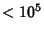 ,
,
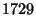 |
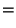 |
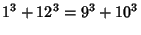 |
(3) |
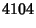 |
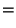 |
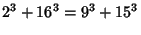 |
(4) |
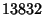 |
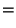 |
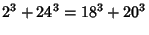 |
(5) |
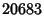 |
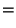 |
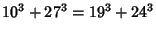 |
(6) |
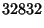 |
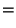 |
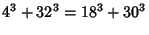 |
(7) |
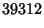 |
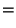 |
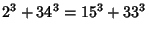 |
(8) |
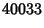 |
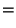 |
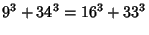 |
(9) |
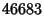 |
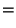 |
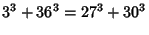 |
(10) |
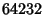 |
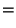 |
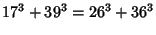 |
(11) |
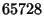 |
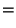 |
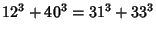 |
(12) |
(Sloane's A001235; Moreau 1898). The first number (Madachy 1979, pp. 124 and 141) in this sequence, the so-called
Hardy-Ramanujan Number, is associated with a story told about Ramanujan  by
G. H. Hardy,
by
G. H. Hardy,  but was known as early as 1657 (Berndt and Bhargava 1993). The smallest number
representable in
but was known as early as 1657 (Berndt and Bhargava 1993). The smallest number
representable in 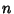 ways as a sum of cubes is called the
ways as a sum of cubes is called the 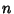 th Taxicab Number.
th Taxicab Number.
Ramanujan  gave a general solution to the 2-2 equation as
gave a general solution to the 2-2 equation as
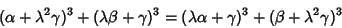 |
(13) |
where
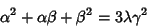 |
(14) |
(Berndt 1994, p. 107). Another form due to Ramanujan is
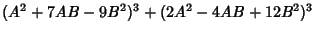
|
|
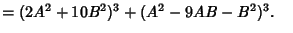
|
(15) |
Hardy and Wright (1979, Theorem 412) prove that there are numbers that are expressible as the sum of two cubes in 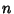 ways for any
ways for any 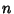 (Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers:
given Rationals Numbers
(Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers:
given Rationals Numbers 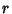 and
and 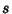 , compute
, compute
Then
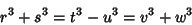 |
(20) |
The Denominators can now be cleared to produce an integer solution. If 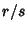 is picked to be
large enough, the
is picked to be
large enough, the 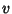 and
and 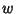 will be Positive. If
will be Positive. If 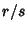 is still larger, the
is still larger, the 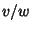 will be large enough for
will be large enough for 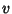 and
and
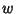 to be used as the inputs to produce a third pair, etc. However, the resulting integers may be quite large, even for
to be used as the inputs to produce a third pair, etc. However, the resulting integers may be quite large, even for
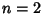 . E.g., starting with
. E.g., starting with
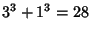 , the algorithm finds
, the algorithm finds
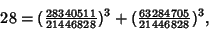 |
(21) |
giving
The numbers representable in three ways as a sum of two cubes (a 2-2-2 equation) are
(Guy 1994, Sloane's A003825). Wilson (1997) found 32 numbers representable in four ways as the sum of two cubes (a
2-2-2-2 equation). The first is
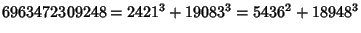
|
|
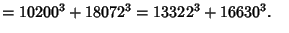
|
(29) |
The smallest known numbers so representable are 6963472309248, 12625136269928, 21131226514944, 26059452841000,
... (Sloane's A003826). Wilson also found six five-way sums,
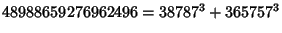
|
|
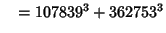
|
|
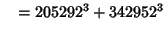
|
|
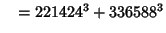
|
|
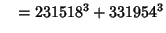
|
(30) |
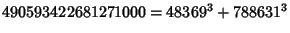
|
|
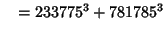
|
|
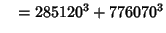
|
|
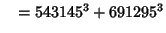
|
|
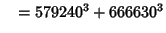
|
(31) |

|
|
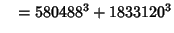
|
|
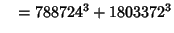
|
|
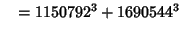
|
|
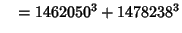
|
(32) |
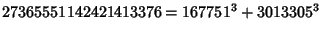
|
|
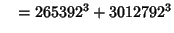
|
|
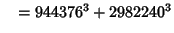
|
|
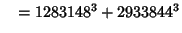
|
|
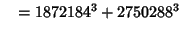
|
(33) |
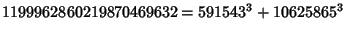
|
|
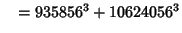
|
|
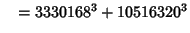
|
|
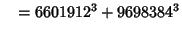
|
|
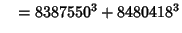
|
(34) |
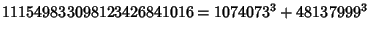
|
|
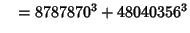
|
|
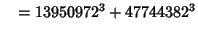
|
|
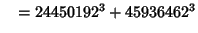
|
|
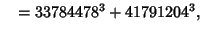
|
(35) |
and a single six-way sum
The first rational solution to the 3-1 equation
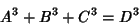 |
(37) |
was found by Euler and Vieta (Dickson 1966, pp. 550-554). Hardy and Wright (1979, pp. 199-201) give a solution which
can be based on the identities
This is equivalent to the general 2-2 solution found by Ramanujan  (Berndt 1994, pp. 54 and 107). The smallest integral
solutions are
(Berndt 1994, pp. 54 and 107). The smallest integral
solutions are
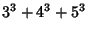 |
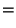 |
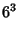 |
(40) |
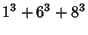 |
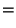 |
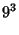 |
(41) |
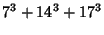 |
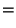 |
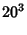 |
(42) |
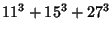 |
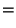 |
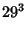 |
(43) |
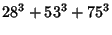 |
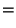 |
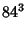 |
(44) |
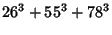 |
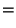 |
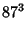 |
(45) |
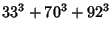 |
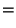 |
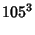 |
(46) |
(Beeler et al. 1972; Madachy 1979, pp. 124 and 141). Other general solutions have been found by Binet (1841) and Schwering
(1902), although Ramanujan's  formulation is the simplest. No general solution giving all
Positive integral solutions is known (Dickson 1966, pp. 550-561).
formulation is the simplest. No general solution giving all
Positive integral solutions is known (Dickson 1966, pp. 550-561).
4-1 equations include
A solution to the 4-4 equation is
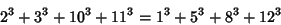 |
(49) |
(Madachy 1979, pp. 118 and 133).
5-1 equations
and a 6-1 equation is given by
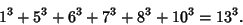 |
(52) |
A 6-6 equation also exists:
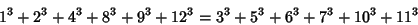 |
(53) |
(Madachy 1979, p. 142).
Euler  gave the general solution to
gave the general solution to
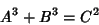 |
(54) |
as
See also Cannonball Problem, Hardy-Ramanujan Number,
Super-3 Number, Taxicab Number, Trimorphic Number
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. Item 58 in HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239,
Feb. 1972.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Berndt, B. C. and Bhargava, S. ``Ramanujan--For Lowbrows.'' Amer. Math. Monthly 100, 645-656, 1993.
Binet, J. P. M. ``Note sur une question relative à la théorie des nombres.'' C. R. Acad. Sci. (Paris) 12, 248-250, 1841.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1966.
Guy, R. K. ``Sums of Like Powers. Euler's Conjecture.'' §D1 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 68,
1959.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, 1979.
Moreau, C. ``Plus petit nombre égal à la somme de deux cubes de deux façons.'' L'Intermediaire Math. 5, 66, 1898.
Schwering, K. ``Vereinfachte Lösungen des Eulerschen Aufgabe:
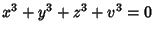 .'' Arch. Math. Phys. 2, 280-284, 1902.
.'' Arch. Math. Phys. 2, 280-284, 1902.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 157, 1993.
Sloane, N. J. A.
A001235 and
A003825
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Wilson, D. Personal communication, Apr. 17, 1997.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() gave a general solution to the 2-2 equation as
gave a general solution to the 2-2 equation as
![]() ways for any
ways for any ![]() (Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers:
given Rationals Numbers
(Guy 1994, pp. 140-141). The proof is constructive, providing a method for computing such numbers:
given Rationals Numbers ![]() and
and ![]() , compute
, compute
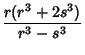
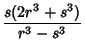
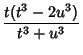
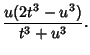
![]() gave the general solution to
gave the general solution to
![]() .'' Arch. Math. Phys. 2, 280-284, 1902.
.'' Arch. Math. Phys. 2, 280-284, 1902.