|
|
|
An equation of the form
| (1) |
| (2) |
| (3) |
If ![]() is Odd, then
is Odd, then ![]() is Positive and the solution in terms of smallest Integers is
is Positive and the solution in terms of smallest Integers is ![]() and
and ![]() , where
, where ![]() is the
is the ![]() th Convergent. If
th Convergent. If ![]() is Even, then
is Even, then ![]() is Negative, but
is Negative, but
| (4) |
| (5) |
The more complicated equation
| (6) |
| (7) |
| (8) |
Call a Diophantine equation consisting of finding ![]() Powers equal to a sum of
Powers equal to a sum of ![]() equal
Powers an ``
equal
Powers an ``![]() equation.'' The 2-1 equation
equation.'' The 2-1 equation
| (9) |
| (10) |
| (11) |
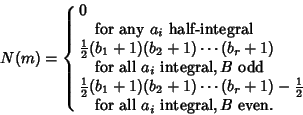 |
(12) |
If zero is counted as a square, both Positive and Negative numbers are included, and the order of the two squares is
distinguished, Jacobi ![]() showed that the number of ways a number can be written as the sum of two squares is four times the
excess of the number of Divisors of the form
showed that the number of ways a number can be written as the sum of two squares is four times the
excess of the number of Divisors of the form ![]() over the number of Divisors of
the form
over the number of Divisors of
the form ![]() .
.
A set of Integers satisfying the 3-1 equation
| (13) |
| (14) |
Solutions to an equation of the form
| (15) |
| (16) |
| (17) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(18) |
| (19) |
See also Algebra, Cannonball Problem, Continued Fraction, Fermat Difference Equation, Lagrange Number (Diophantine Equation), Pell Equation, Pythagorean Quadruple, Pythagorean Triple, Quadratic Residue
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Beiler, A. H. ``The Pellian.'' Ch. 22 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains.
New York: Dover, pp. 248-268, 1966.
Bell, E. T. The Development of Mathematics, 2nd ed. New York: McGraw-Hill, p. 159, 1945.
Chrystal, G. Textbook of Algebra, 2 vols. New York: Chelsea, 1961.
Degan, C. F. Canon Pellianus. Copenhagen, Denmark, 1817.
Dickson, L. E. ``Number of Representations as a Sum of 5, 6, 7, or 8 Squares.'' Ch. 13 in
Studies in the Theory of Numbers. Chicago, IL: University of Chicago Press, 1930.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1966.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Lam, T. Y. The Algebraic Theory of Quadratic Forms. Reading, MA: W. A. Benjamin, 1973.
Rajwade, A. R. Squares. Cambridge, England: Cambridge University Press, 1993.
Scharlau, W. Quadratic and Hermitian Forms. Berlin: Springer-Verlag, 1985.
Shapiro, D. B. ``Products of Sums and Squares.'' Expo. Math. 2, 235-261, 1984.
Smarandache, F. ``Un metodo de resolucion de la ecuacion diofantica.'' Gaz. Math. 1, 151-157, 1988.
Smarandache, F. ``Method to Solve the Diophantine Equation
Taussky, O. ``Sums of Squares.'' Amer. Math. Monthly 77, 805-830, 1970.
Whitford, E. E. Pell Equation. New York: Columbia University Press, 1912.
![]() .'' In Collected Papers, Vol. 1.
Bucharest, Romania: Tempus, 1996.
.'' In Collected Papers, Vol. 1.
Bucharest, Romania: Tempus, 1996.
|
|
|
© 1996-9 Eric W. Weisstein