|
|
|
The study of Angles and of the angular relationships of planar and 3-D figures is known as trigonometry.
The trigonometric functions (also called the Circular Functions) comprising trigonometry are the Cosecant
![]() , Cosine
, Cosine ![]() , Cotangent
, Cotangent ![]() , Secant
, Secant ![]() , Sine
, Sine ![]() , and
Tangent
, and
Tangent ![]() . The inverses of these functions are denoted
. The inverses of these functions are denoted ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and ![]() . Note that the
. Note that the ![]() Notation here means Inverse
Function, not
Notation here means Inverse
Function, not ![]() to the
to the ![]() Power.
Power.
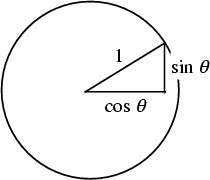
The trigonometric functions are most simply defined using the Unit Circle. Let ![]() be an Angle measured
counterclockwise from the x-Axis along an Arc of the Circle. Then
be an Angle measured
counterclockwise from the x-Axis along an Arc of the Circle. Then ![]() is the horizontal
coordinate of the Arc endpoint, and
is the horizontal
coordinate of the Arc endpoint, and ![]() is the vertical component. The Ratio
is the vertical component. The Ratio
![]() is defined as
is defined as ![]() . As a result of this definition, the trigonometric functions are
periodic with period
. As a result of this definition, the trigonometric functions are
periodic with period ![]() , so
, so
| (1) |
From the Pythagorean Theorem,
| (2) |
| (3) |
| (4) |
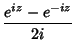 |
(5) | ||
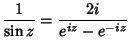 |
(6) | ||
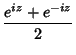 |
(7) | ||
| (8) | |||
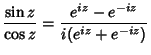 |
(9) | ||
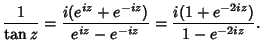 |
(10) |
Osborne's Rule gives a prescription for converting trigonometric identities to analogous identities for Hyperbolic Functions.
The Angles ![]() (with
(with ![]() integers) for which the trigonometric function may be expressed in terms
of finite root extraction of real numbers are limited to values of
integers) for which the trigonometric function may be expressed in terms
of finite root extraction of real numbers are limited to values of ![]() which are precisely those which produce
constructible Polygons. Gauß
which are precisely those which produce
constructible Polygons. Gauß ![]() showed these to be of the form
showed these to be of the form
| (11) |
| 0.0 | 0 | 0 | 1 | 0 |
| 15.0 |
|
|
|
|
| 18.0 |
|
|
|
|
| 22.5 |
|
|
|
|
| 30.0 |
|
|
|
|
| 36.0 |
|
|
|
|
| 45.0 |
|
|
|
1 |
| 60.0 |
|
|
|
|
| 90.0 |
|
1 | 0 | |
| 180.0 | 0 | 0 |
The Inverse Trigonometric Functions are generally defined on the following domains.
| Function | Domain |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Inverse-forward identities are
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
Inverse sum identities include
| (20) |
| (21) |
| (22) |
| (23) |
Complex inverse identities in terms of Logarithms include
| (24) | |||
| (25) | |||
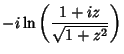 |
(26) | ||
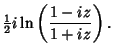 |
(27) |
For Imaginary arguments,
| (28) | |||
| (29) |
| (30) | |||
| (31) |
| (32) | |||
| (33) |
| (34) |
| (35) |
Trigonometric product formulas can be derived using the following figure (Kung 1996).
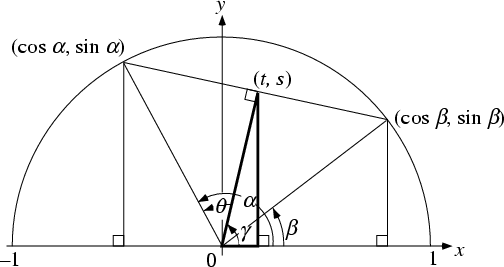
In the figure,
| (36) | |||
| (37) |
| (38) | |||
| (39) |
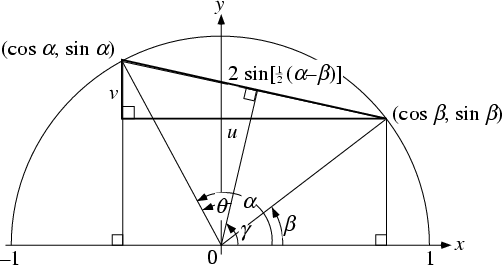
With ![]() and
and ![]() as previously defined, the above figure (Kung 1996) gives
as previously defined, the above figure (Kung 1996) gives
| (40) | |||
| (41) |
Angle addition Formulas express trigonometric functions of sums of angles
![]() in terms of functions of
in terms of functions of ![]() and
and ![]() . They can be simply derived using Complex
exponentials and the Euler Formula,
. They can be simply derived using Complex
exponentials and the Euler Formula,
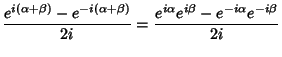 |
|||
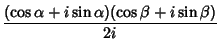 |
|||
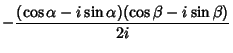 |
|||
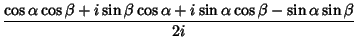 |
|||
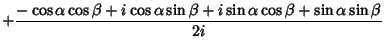 |
|||
| (42) |
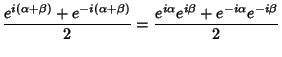 |
|||
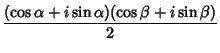 |
|||
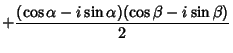 |
|||
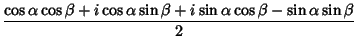 |
|||
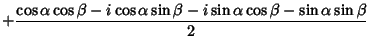 |
|||
| (43) |
Taking the ratio gives the tangent angle addition Formula
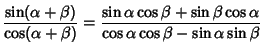 |
|||
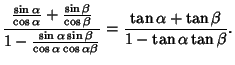 |
(44) |
The angle addition Formulas can also be derived purely algebraically without the use of Complex Numbers. Consider the following figure.
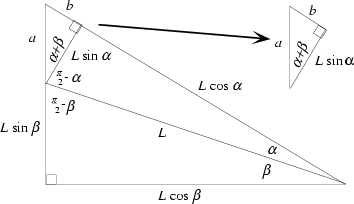
From the large Right Triangle,
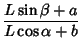 |
(45) | ||
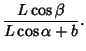 |
(46) |
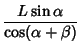 |
(47) | ||
| (48) |
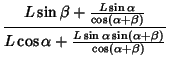 |
|||
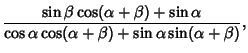 |
|||
| (49) |
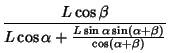 |
|||
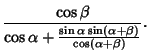 |
(50) |
| (51) |
| (52) |
![$\sin(\alpha+\beta)={\sin\beta\left[{\cos\beta-\sin\alpha\sin(\alpha+\beta)\over...
...in\alpha\sin(\alpha+\beta)\over\cos\alpha}\right]+\sin\alpha\sin(\alpha+\beta)}$](t_1709.gif)
|
|
|
|
|
|
|
|
|
|
(53) |
so
| (54) |
| (55) |
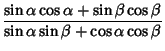 |
|||
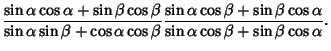 |
(56) |
|
|
|
|
|
|
|
|
|
|
|
(57) |
so
| (58) |
| (59) |
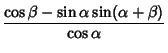 |
|||
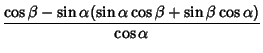 |
|||
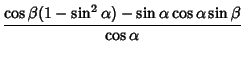 |
|||
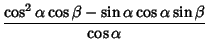 |
|||
| (60) |
Summarizing (and explicitly writing out the identities for which ![]() is taken to be explicitly negative),
is taken to be explicitly negative),
| (61) | |||
| (62) | |||
| (63) | |||
| (64) | |||
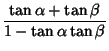 |
(65) | ||
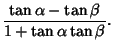 |
(66) |
| (67) |
The double angle formulas are
| (68) | |||
| (69) | |||
| (70) | |||
| (71) | |||
| (72) |
General multiple angle formulas are
|
|
(73) |
|
|
(74) |
|
|
(75) |
|
|
|
|
|
(76) |
|
|
(77) |
| (78) | |||
| (79) | |||
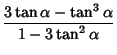 |
(80) | ||
| (81) | |||
| (82) | |||
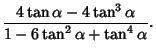 |
(83) |
Sum identities include
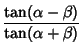 |
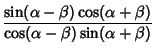 |
||
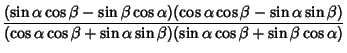 |
|||
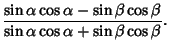 |
(84) |
Infinite sum identities include
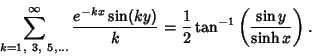 |
(85) |
Trigonometric half-angle formulas include
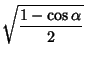 |
(86) | ||
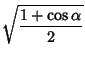 |
(87) | ||
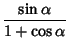 |
(88) | ||
| (89) | |||
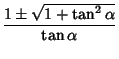 |
(90) | ||
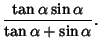 |
(91) |
The Prosthaphaeresis Formulas are
| (92) | |||
| (93) | |||
| (94) | |||
| (95) |
| (96) | |||
| (97) | |||
| (98) | |||
| (99) |
Trigonometric product/sum formulas are
| (100) |
| (101) |
Power formulas include
| (102) | |||
| (103) | |||
| (104) |
| (105) | |||
| (106) | |||
| (107) |
![$\displaystyle {1\over 2^{2n}}{2n\choose n}+{(-1)^n\over 2^{2n-1}}\sum_{k=0}^{n-1} (-1)^k{2n\choose k}\cos[2(n-k)x]\quad\eqnum$](t_1807.gif) |
(108) | ||
![$\displaystyle {(-1)^n\over 4^n}\sum_{k=0}^n (-1)^k{2n+1\choose k}\sin[(2n+1-2k)x]$](t_1809.gif) |
(109) | ||
![$\displaystyle {1\over 2^{2n}}{2n\choose n}+{1\over 2^{2n-1}}\sum_{k=0}^{n-1}{2n\choose k}\cos[2(n-k)x]$](t_1811.gif) |
(110) | ||
![$\displaystyle {1\over 4^n}\sum_{k=0}^n{2n+1\choose k}\cos[(2n+1-2k)x]$](t_1813.gif) |
(111) |
Trigonometric identities which prove useful in the construction of map projections include
|
|
|
|
|
(112) |
| (113) | |||
| (114) | |||
| (115) | |||
| (116) |
|
|
|
|
|
(117) |
| (118) | |||
| (119) | |||
| (120) | |||
| (121) |
|
|
|
|
|
(122) |
where
| (123) | |||
| (124) | |||
| (125) | |||
| (126) | |||
| (127) |
See also Cosecant, Cosine, Cotangent, Euclidean Number, Inverse Cosecant, Inverse Cosine, Inverse Cotangent, Inverse Secant, Inverse Sine, Inverse Tangent, Inverse Trigonometric Functions, Osborne's Rule, Polygon, Secant, Sine, Tangent, Trigonometry Values: Pi, Trigonometry Values: Pi/2, Trigonometry Values: Pi/3, Trigonometry Values: Pi/4, Trigonometry Values: Pi/5, Trigonometry Values: Pi/6, Trigonometry Values: Pi/7, Trigonometry Values: Pi/8, Trigonometry Values: Pi/9, Trigonometry Values: Pi/10, Trigonometry Values: Pi/11, Trigonometry Values: Pi/12, Trigonometry Values: Pi/15, Trigonometry Values: Pi/16, Trigonometry Values: Pi/17, Trigonometry Values: Pi/18, Trigonometry Values: Pi/20, Trigonometry Values 0, Werner Formulas
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Circular Functions.'' §4.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 71-79, 1972.
Bahm, L. B. The New Trigonometry on Your Own. Patterson, NJ: Littlefield, Adams & Co., 1964.
Beyer, W. H. ``Trigonometry.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
pp. 134-152, 1987.
Dixon, R. ``The Story of Sine and Cosine.'' § 4.4 in Mathographics. New York: Dover, pp. 102-106, 1991.
Hobson, E. W. A Treatise on Plane Trigonometry. London: Cambridge University Press, 1925.
Kells, L. M.; Kern, W. F.; and Bland, J. R. Plane and Spherical Trigonometry. New York: McGraw-Hill, 1940.
Kogan, S. ``A Note on Definite Integrals Involving Trigonometric Functions.''
http://www.mathsoft.com/asolve/constant/pi/sin/sin.html.
Kung, S. H. ``Proof Without Words: The Difference-Product Identities'' and
``Proof Without Words: The Sum-Product Identities.'' Math. Mag. 69, 269, 1996.
Maor, E. Trigonometric Delights. Princeton, NJ: Princeton University Press, 1998.
Morrill, W. K. Plane Trigonometry, rev. ed. Dubuque, IA: Wm. C. Brown, 1964.
Robinson, R. M. ``A Curious Mathematical Identity.'' Amer. Math. Monthly 64, 83-85, 1957.
Sloane, N. J. A. Sequence
A003401/M0505
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395.
Washington, DC: U. S. Government Printing Office, p. 19, 1987.
Thompson, J. E. Trigonometry for the Practical Man. Princeton, NJ: Van Nostrand.
Yates, R. C. ``Trigonometric Functions.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 225-232, 1952.
Zill, D. G. and Dewar, J. M. Trigonometry, 2nd ed. New York: McGraw-Hill 1990.
![]() Trigonometry
Trigonometry
![]() Weisstein, E. W. ``Exact Values of Trigonometric Functions.'' Mathematica notebook TrigExact.m.
Weisstein, E. W. ``Exact Values of Trigonometric Functions.'' Mathematica notebook TrigExact.m.
|
|
|
© 1996-9 Eric W. Weisstein