|
|
|
For a Right Triangle with legs ![]() and
and ![]() and Hypotenuse
and Hypotenuse ![]() ,
,
| (1) |
A clever proof by Dissection which reassembles two small squares into one larger one was given by the Arabian
mathematician Thabit Ibn Qurra ![]() (Ogilvy 1994, Frederickson 1997).
(Ogilvy 1994, Frederickson 1997).
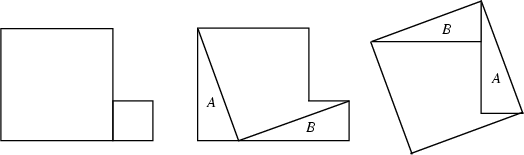
Another proof by Dissection is due to Perigal (Pergial 1873, Dudeney 1970, Madachy 1979, Ball and Coxeter 1987).
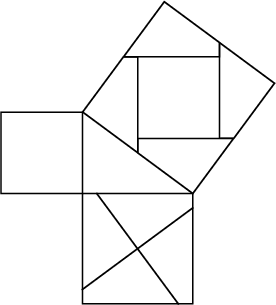
The Indian mathematician Bhaskara constructed a proof using the following figure.

Another beautiful dissection proof is shown below.
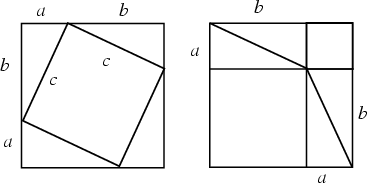
| (2) |
| (3) |
| (4) |
In the above figure, the Area of the large Square is four times the Area of one of the
Triangles plus the Area of the interior Square. From the figure, ![]() , so
, so
| (5) |
Perhaps the most famous proof of all times is Euclid's ![]() geometric proof. Euclid's proof used the figure
below, which is sometimes known variously as the Bride's Chair, Peacock's Tail, or Windmill.
geometric proof. Euclid's proof used the figure
below, which is sometimes known variously as the Bride's Chair, Peacock's Tail, or Windmill.
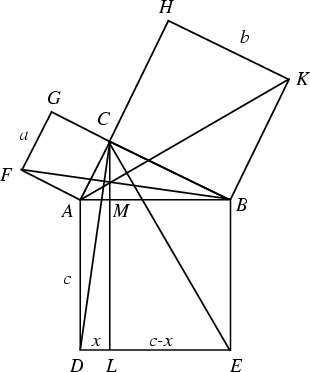
Let ![]() be a Right Triangle,
be a Right Triangle,
![]() ,
,
![]() , and
, and
![]() be squares, and
be squares, and ![]() . The
Triangles
. The
Triangles ![]() and
and ![]() are equivalent except for rotation, so
are equivalent except for rotation, so
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
Heron's Formula for the Area of the Triangle, contains the Pythagorean theorem implicitly. Using the
form
| (11) |
| (12) |
| (13) |
| (14) |
A novel proof using a Trapezoid was discovered by James Garfield (1876), later president of the United States, while serving in the House of Representatives (Pappas 1989, pp. 200-201; Bogomolny).
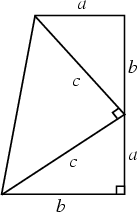
| (15) |
| (16) |
| (17) |
| (18) |
An algebraic proof (which would not have been accepted by the Greeks) uses the Euler Formula. Let the sides of a
Triangle be ![]() ,
, ![]() , and
, and ![]() , and the Perpendicular legs of Right Triangle be aligned along the real
and imaginary axes. Then
, and the Perpendicular legs of Right Triangle be aligned along the real
and imaginary axes. Then
| (19) |
| (20) |
| (21) |
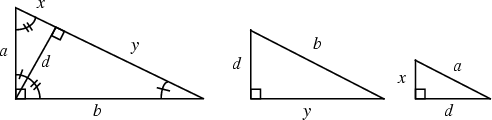
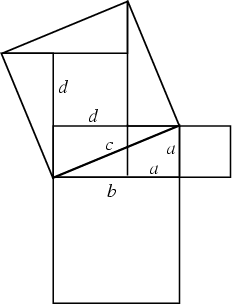
It is a property of Right Triangles, such as the one shown in the above left figure, that the
Right Triangle with sides ![]() ,
, ![]() , and
, and ![]() (small triangle in the left figure; reproduced in the right figure) is
similar to the Right Triangle with sides
(small triangle in the left figure; reproduced in the right figure) is
similar to the Right Triangle with sides ![]() ,
, ![]() , and
, and ![]() (large triangle in the left figure; reproduced in the middle
figure), giving
(large triangle in the left figure; reproduced in the middle
figure), giving
| (22) |
| (23) |
| (24) |
| (25) |
See also Bride's Chair, Cosines Law, Peacock's Tail, Pythagoras's Theorem, Windmill
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 87-88, 1987.
Bogomolny, A. ``Pythagorean Theorem.''
http://www.cut-the-knot.com/pythagoras/index.html.
Dixon, R. ``The Theorem of Pythagoras.'' §4.1 in Mathographics. New York: Dover, pp. 92-95, 1991.
Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 32, 1958.
Dunham, W. ``Euclid's Proof of the Pythagorean Theorem.'' Ch. 2 in
Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, 1990.
Frederickson, G. Dissections: Plane and Fancy. New York: Cambridge University Press, pp. 28-29, 1997.
Garfield, J. A. ``Pons Asinorum.'' New England J. Educ. 3, 161, 1876.
Loomis, E. S. The Pythagorean Proposition: Its Demonstration Analyzed and Classified and Bibliography of Sources for Data of the Four Kinds of ``Proofs.''
Reston, VA: National Council of Teachers of Mathematics, 1968.
Machover, M. ``Euler's Theorem Implies the Pythagorean Proposition.'' Amer. Math. Monthly 103, 351, 1996.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 17, 1979.
Ogilvy, C. S. Excursions in Mathematics. New York: Dover, p. 52, 1994.
Pappas, T. ``The Pythagorean Theorem,'' ``A Twist to the Pythagorean Theorem,'' and ``The Pythagorean Theorem and President Garfield.''
The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 4, 30, and 200-201, 1989.
Perigal, H. ``On Geometric Dissections and Transformations.'' Messenger Math. 2, 103-106, 1873.
Project Mathematics! The Theorem of Pythagoras. Videotape (22 minutes). California Institute of
Technology. Available from the Math. Assoc. Amer.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 123-127, 1993.
Yancey, B. F. and Calderhead, J. A. ``New and Old Proofs of the Pythagorean Theorem.'' Amer. Math. Monthly
3, 65-67, 110-113, 169-171, and 299-300, 1896.
Yancey, B. F. and Calderhead, J. A. ``New and Old Proofs of the Pythagorean Theorem.'' Amer. Math. Monthly
4, 11-12, 79-81, 168-170, 250-251, and 267-269, 1897.
Yancey, B. F. and Calderhead, J. A. ``New and Old Proofs of the Pythagorean Theorem.'' Amer. Math. Monthly 5, 73-74, 1898.
Yancey, B. F. and Calderhead, J. A. ``New and Old Proofs of the Pythagorean Theorem.'' Amer. Math. Monthly 6, 33-34 and 69-71, 1899.
|
|
|
© 1996-9 Eric W. Weisstein