|
|
|
The Euler formula states
| (1) |
| (2) |
| (3) |
The Euler formula can be demonstrated using a series expansion
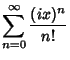 |
|||
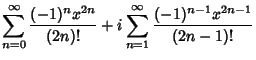 |
|||
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
See also de Moivre's Identity, Euler Polyhedral Formula
References
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. ``Euler's Wonderful Relation.'' The Book of Numbers. New York: Springer-Verlag,
pp. 254-256, 1996.
Cotes, R. Philosophical Transactions 29, 32, 1714.
Euler, L. Miscellanea Berolinensia 7, 179, 1743.
Euler, L. Introductio in Analysin Infinitorum, Vol. 1. Lausanne, p. 104, 1748.
|
|
|
© 1996-9 Eric W. Weisstein