|
|
|
A number which cannot be expressed as a Fraction ![]() for any Integers
for any Integers ![]() and
and ![]() . Every
Transcendental Number is irrational. Numbers of the form
. Every
Transcendental Number is irrational. Numbers of the form ![]() are irrational unless
are irrational unless ![]() is the
is the ![]() th Power
of an Integer.
th Power
of an Integer.
Numbers of the form ![]() , where
, where ![]() is the Logarithm, are irrational if
is the Logarithm, are irrational if ![]() and
and ![]() are Integers, one of which has a Prime factor which the other lacks.
are Integers, one of which has a Prime factor which the other lacks. ![]() is irrational for
rational
is irrational for
rational ![]() . The irrationality of
. The irrationality of ![]() was proven by Lambert
was proven by Lambert ![]() in 1761; for the general case, see Hardy
and Wright (1979, p. 46).
in 1761; for the general case, see Hardy
and Wright (1979, p. 46). ![]() is irrational for Positive integral
is irrational for Positive integral ![]() . The irrationality of
. The irrationality of ![]() was proven by
Lambert
was proven by
Lambert ![]() in 1760; for the general case, see Hardy and Wright (1979, p. 47). Apéry's Constant
in 1760; for the general case, see Hardy and Wright (1979, p. 47). Apéry's Constant ![]() (where
(where ![]() is the Riemann Zeta Function) was proved irrational by Apéry (Apéry 1979,
van der Poorten 1979).
is the Riemann Zeta Function) was proved irrational by Apéry (Apéry 1979,
van der Poorten 1979).
From Gelfond's Theorem, a number of the form ![]() is Transcendental (and therefore
irrational) if
is Transcendental (and therefore
irrational) if ![]() is Algebraic
is Algebraic ![]() , 1 and
, 1 and ![]() is irrational and Algebraic. This establishes the irrationality of
is irrational and Algebraic. This establishes the irrationality of ![]() (since
(since
![]() ),
), ![]() , and
, and ![]() .
Nesterenko (1996) proved that
.
Nesterenko (1996) proved that ![]() is irrational. In fact, he proved that
is irrational. In fact, he proved that ![]() ,
, ![]() and
and ![]() are
algebraically independent, but it was not previously known that
are
algebraically independent, but it was not previously known that ![]() was irrational.
was irrational.
Given a Polynomial equation
| (1) |
Irrationality has not yet been established for ![]() ,
, ![]() ,
,
![]() , or
, or ![]() (where
(where ![]() is the
Euler-Mascheroni Constant).
is the
Euler-Mascheroni Constant).
Quadratic Surds are irrational numbers which have periodic Continued Fractions.
Hurwitz's Irrational Number Theorem gives bounds of the form
| (2) |
The Series
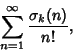 |
(3) |
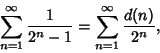 |
(4) |
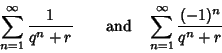 |
(5) |
See also Algebraic Integer, Algebraic Number, Almost Integer, Dirichlet Function, Ferguson-Forcade Algorithm, Gelfond's Theorem, Hurwitz's Irrational Number Theorem, Near Noble Number, Noble Number, Pythagoras's Theorem, Quadratic Irrational Number, Rational Number, Segre's Theorem, Transcendental Number
References
Apéry, R. ``Irrationalité de
Courant, R. and Robbins, H. ``Incommensurable Segments, Irrational Numbers, and the Concept of Limit.'' §2.2 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 58-61, 1996.
Guy, R. K. ``Some Irrational Series.'' §B14 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 69, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Clarendon Press, 1979.
Manning, H. P. Irrational Numbers and Their Representation by Sequences and Series. New York: Wiley, 1906.
Nesterenko, Yu. ``Modular Functions and Transcendence Problems.'' C. R. Acad. Sci. Paris Sér. I Math.
322, 909-914, 1996.
Nesterenko, Yu. V. ``Modular Functions and Transcendence Questions.'' Mat. Sb. 187, 65-96, 1996.
Niven, I. M. Irrational Numbers. New York: Wiley, 1956.
Niven, I. M. Numbers: Rational and Irrational. New York: Random House, 1961.
Pappas, T. ``Irrational Numbers & the Pythagoras Theorem.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 98-99, 1989.
van der Poorten, A. ``A Proof that Euler Missed... Apéry's Proof of the Irrationality of
![]() Irrational Numbers
Irrational Numbers
![]() et
et ![]() .'' Astérisque 61, 11-13, 1979.
.'' Astérisque 61, 11-13, 1979.
![]() .''
Math. Intel. 1, 196-203, 1979.
.''
Math. Intel. 1, 196-203, 1979.
|
|
|
© 1996-9 Eric W. Weisstein