Amdeberhan, T. ``Faster and Faster Convergent Series for 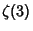 .'' Electronic J. Combinatorics 3, R13 1-2, 1996.
http://www.combinatorics.org/Volume_3/volume3.html#R13.
.'' Electronic J. Combinatorics 3, R13 1-2, 1996.
http://www.combinatorics.org/Volume_3/volume3.html#R13.
Amdeberhan, T. and Zeilberger, D. ``Hypergeometric Series Acceleration via the WZ Method.'' Electronic J. Combinatorics 4, No. 2, R3, 1-3, 1997.
http://www.combinatorics.org/Volume_4/wilftoc.html#R03. Also available at
http://www.math.temple.edu/~zeilberg/mamarim/mamarimhtml/accel.html.
Apéry, R. ``Irrationalité de 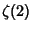 et
et 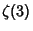 .'' Astérisque 61, 11-13, 1979.
.'' Astérisque 61, 11-13, 1979.
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, 1985.
Beukers, F. ``A Note on the Irrationality of 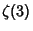 .'' Bull. London Math. Soc. 11, 268-272, 1979.
.'' Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. ``The Great Enigma.'' In The Book of Numbers. New York: Springer-Verlag,
pp. 261-262, 1996.
Ewell, J. A. ``A New Series Representation for  .'' Amer. Math. Monthly 97, 219-220, 1990.
.'' Amer. Math. Monthly 97, 219-220, 1990.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/apery/apery.html
Gosper, R. W. ``Strip Mining in the Abandoned Orefields of Nineteenth Century Mathematics.'' In Computers in Mathematics
(Ed. D. V. Chudnovsky and R. D. Jenks). New York: Marcel Dekker, 1990.
Haible, B. and Papanikolaou, T. ``Fast Multiprecision Evaluation of Series of Rational Numbers.'' Technical Report TI-97-7.
Darmstadt, Germany: Darmstadt University of Technology, Apr. 1997.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 36, 1983.
Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computation
of Constants.'' http://www.lacim.uqam.ca/pi/records.html.
Sloane, N. J. A.
A013631,
A033165, and
A002117/M0020
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
van der Poorten, A. ``A Proof that Euler Missed... Apéry's Proof of the Irrationality of  .'' Math. Intel. 1,
196-203, 1979.
.'' Math. Intel. 1,
196-203, 1979.
Zeilberger, D. ``The Method of Creative Telescoping.'' J. Symb. Comput. 11, 195-204, 1991.
![]() are
are
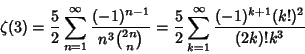
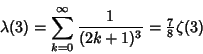
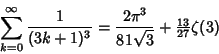
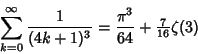
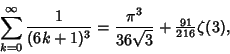
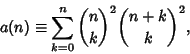
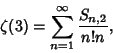
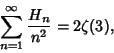
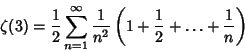
![]() include
include
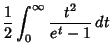
![$\displaystyle {8\over 7}\left[{{\textstyle{1\over 4}}\pi^2\ln 2+2\int_0^{\pi/4} x\ln(\sin x)\,dx}\right].$](a_1135.gif)
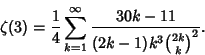
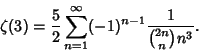
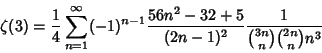
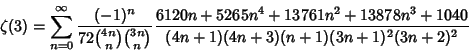
![\begin{displaymath}
\lim_{N\to\infty} \prod_{n=1}^N M_n = \left[{\matrix{0 & \zeta(3)\cr 0 & 1\cr}}\right],
\end{displaymath}](a_1149.gif)
![\begin{displaymath}
M_n\equiv\left[{\matrix{ {(n+1)^4\over 4096(n+{\textstyle{5\...
...le{1\over 2}})(n+{\textstyle{2\over 3}})}\cr 0 & 1\cr}}\right]
\end{displaymath}](a_1150.gif)
![$\displaystyle \left[\begin{array}{cc}{\textstyle{1\over 19600}} & {\textstyle{2077\over 1728}}\\ 0 & 1\end{array}\right]$](a_1152.gif)
![$\displaystyle \left[\begin{array}{cc}{\textstyle{1\over 9801}} & {\textstyle{7561\over 4320}}\\ 0 & 1\end{array}\right]$](a_1154.gif)
![$\displaystyle \left[\begin{array}{cc}{\textstyle{9\over 67600}} & {\textstyle{50501\over 20160}}\\ 0 & 1\end{array}\right],$](a_1156.gif)
![]() to 1,000,000 Digits using a Wilf-Zeilberger
Pair identity with
to 1,000,000 Digits using a Wilf-Zeilberger
Pair identity with
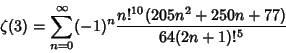
![]() .'' Electronic J. Combinatorics 3, R13 1-2, 1996.
http://www.combinatorics.org/Volume_3/volume3.html#R13.
.'' Electronic J. Combinatorics 3, R13 1-2, 1996.
http://www.combinatorics.org/Volume_3/volume3.html#R13.
![]() et
et ![]() .'' Astérisque 61, 11-13, 1979.
.'' Astérisque 61, 11-13, 1979.
![]() .'' Bull. London Math. Soc. 11, 268-272, 1979.
.'' Bull. London Math. Soc. 11, 268-272, 1979.
![]() .'' Amer. Math. Monthly 97, 219-220, 1990.
.'' Amer. Math. Monthly 97, 219-220, 1990.
![]() .'' Math. Intel. 1,
196-203, 1979.
.'' Math. Intel. 1,
196-203, 1979.