Borwein, D. and Borwein, J. M. ``On an Intriguing Integral and Some Series Related to 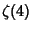 .''
Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
.''
Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 143 and 258-259, 1996.
de Doelder, P. J. ``On Some Series Containing
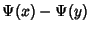 and
and
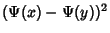 for Certain Values
of
for Certain Values
of 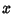 and
and 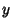 .'' J. Comp. Appl. Math. 37, 125-141, 1991.
.'' J. Comp. Appl. Math. 37, 125-141, 1991.
Roman, S. ``The Logarithmic Binomial Formula.'' Amer. Math. Monthly 99, 641-648, 1992.
Sloane, N. J. A. Sequences
A001008/M2885
and A002805/M1589
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
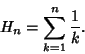
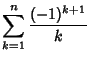
![\begin{displaymath}
\sum_{i=0}^\infty {z^i H_i\over i!} = -e^z\sum_{k=1}^\infty {(-z)^k\over kk!} = e^z[\ln z+\Gamma(0,z)+\gamma],
\end{displaymath}](h_519.gif)
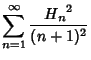
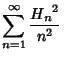
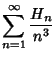
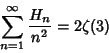
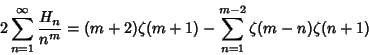
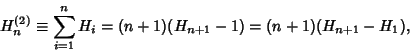
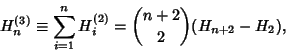
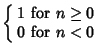
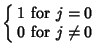
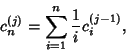
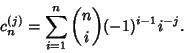
![]() .''
Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
.''
Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
![]() and
and
![]() for Certain Values
of
for Certain Values
of ![]() and
and ![]() .'' J. Comp. Appl. Math. 37, 125-141, 1991.
.'' J. Comp. Appl. Math. 37, 125-141, 1991.