|
|
|
The Sum
| (1) |
| (2) |
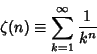 |
(3) |
The sum of the first few terms of the harmonic series is given analytically by the ![]() th Harmonic Number
th Harmonic Number
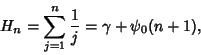 |
(4) |
Progressions of the form
| (5) |
See also Arithmetic Series, Bernoulli's Paradox, Book Stacking Problem, Euler Sum, Zipf's Law
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 279-280, 1985.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.
Boas, R. P. and Wrench, J. W. ``Partial Sums of the Harmonic Series.'' Amer. Math. Monthly 78, 864-870, 1971.
Honsberger, R. ``An Intriguing Series.'' Ch. 10 in Mathematical Gems II.
Washington, DC: Math. Assoc. Amer., pp. 98-103, 1976.
Sloane, N. J. A. Sequence
A004080
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein