|
|
|
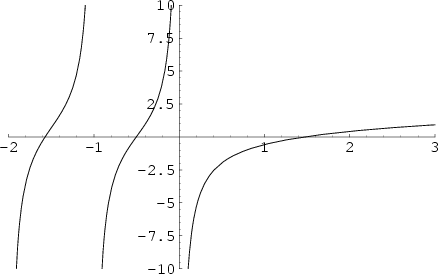
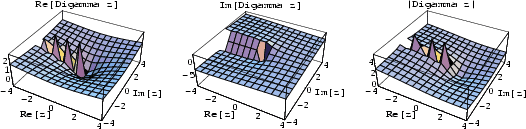
Two notations are used for the digamma function. The ![]() digamma function is defined by
digamma function is defined by
| (1) |
| (2) |
| (3) |
![$\displaystyle {d\over dz} \lim_{n\to \infty} [\ln n!+z\ln n-\ln (z+1)-\ln (z+2)-\ldots -\ln (z+n)]$](d1_872.gif) |
(4) | ||
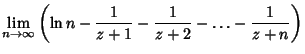 |
|||
| (5) | |||
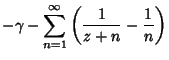 |
(6) | ||
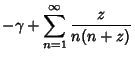 |
(7) | ||
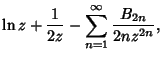 |
(8) |
The ![]() th Derivative of
th Derivative of ![]() is called the Polygamma Function and is denoted
is called the Polygamma Function and is denoted ![]() . Since the
digamma function is the zeroth derivative of
. Since the
digamma function is the zeroth derivative of ![]() (i.e., the function itself), it is also denoted
(i.e., the function itself), it is also denoted ![]() .
.
The digamma function satisfies
| (9) |
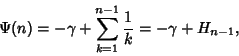 |
(10) |
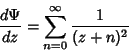 |
(11) |
| (12) |
| (13) |
| (14) |
Special values are
| (15) | |||
| (16) |
At integral values,
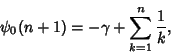 |
(17) |
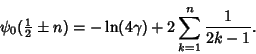 |
(18) |
![\begin{displaymath}
\psi_0\left({p\over q}\right)=-\gamma-\ln(2q)-{\textstyle{1\...
...ver q}\right)\ln\left[{\sin\left({\pi k\over q}\right)}\right]
\end{displaymath}](d1_895.gif) |
(19) |
| (20) | |||
| (21) | |||
| (22) | |||
| (23) | |||
| (24) | |||
| (25) |
See also Gamma Function, Harmonic Number, Hurwitz Zeta Function, Polygamma Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Psi (Digamma) Function.'' §6.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 258-259, 1972.
Arfken, G. ``Digamma and Polygamma Functions.'' §10.2 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 549-555, 1985.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, p. 94, 1973.
Spanier, J. and Oldham, K. B. ``The Digamma Function
![]() .''
Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
.''
Ch. 44 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 423-434, 1987.
|
|
|
© 1996-9 Eric W. Weisstein