Abramowitz, M. and Stegun, C. A. (Eds.). ``Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula.''
§23.1 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Arfken, G. ``Bernoulli Numbers, Euler-Maclaurin Formula.'' §5.9 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338,
1985.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, p. 71, 1987.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 81-85, 1994.
Boyer, C. B. A History of Mathematics. New York: Wiley, 1968.
Castellanos, D. ``The Ubiquitous Pi. Part I.'' Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 107-110, 1996.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed.
San Diego, CA: Academic Press, 1980.
Hardy, G. H. and Wright, W. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford
University Press, pp. 91-93, 1979.
Ireland, K. and Rosen, M. ``Bernoulli Numbers.'' Ch. 15 in A Classical Introduction to Modern Number
Theory, 2nd ed. New York: Springer-Verlag, pp. 228-248, 1990.
Knuth, D. E. and Buckholtz, T. J. ``Computation of Tangent, Euler, and Bernoulli Numbers.'' Math. Comput.
21, 663-688, 1967.
Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computation
of Constants.'' http://www.lacim.uqam.ca/pi/records.html.
Ramanujan, S. ``Some Properties of Bernoulli's Numbers.'' J. Indian Math. Soc. 3, 219-234, 1911.
Sloane, N. J. A. Sequences
A000367/M4039
and A002445/M4189
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Spanier, J. and Oldham, K. B. ``The Bernoulli Numbers, 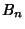 .''
Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
.''
Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
Wagstaff, S. S. Jr. ``Ramanujan's Paper on Bernoulli Numbers.'' J. Indian Math. Soc. 45, 49-65, 1981.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
![]() by the equations
by the equations
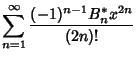
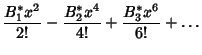
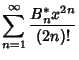
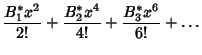
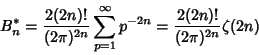
![]() are
are
![]() and also called ``Even-index'' Bernoulli numbers. These are
the Bernoulli numbers returned by the Mathematica
and also called ``Even-index'' Bernoulli numbers. These are
the Bernoulli numbers returned by the Mathematica
![]() (Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones
(Wolfram Research, Champaign, IL) function BernoulliB[n]. These Bernoulli numbers are a superset of the archaic ones ![]() since
since
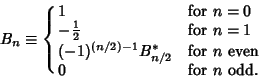
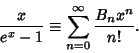
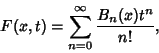
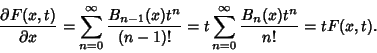
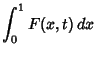
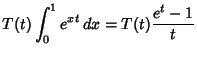
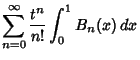
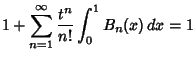
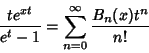
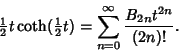
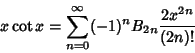
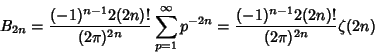
![]() is given by the von Staudt-Clausen Theorem
is given by the von Staudt-Clausen Theorem
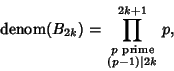
![]() . He used the property of the Figurate
Number Triangle that
. He used the property of the Figurate
Number Triangle that
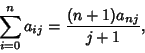
![\begin{displaymath}
\sum_{k=1}^n k^p = {(B+n+1)^{[p+1]}-B^{p+1}\over p+1},
\end{displaymath}](b_618.gif)
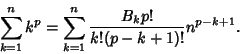
![]() , which has
, which has ![]() Digits (Plouffe). Plouffe
and collaborators have also calculated
Digits (Plouffe). Plouffe
and collaborators have also calculated ![]() for
for ![]() up to 72,000.
up to 72,000.
![]() .''
Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
.''
Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.