Genocchi Number

A number given by the Generating Function

$${2t\over e^t+1}=\sum_{n=1}^\infty G_n {t^n\over n!}.$$

It satisfies $G_1=1$, $G_3=G_5=G_7=\ldots=0$, and even coefficients are given by

$$G_{2n} = 2(1-2^{2n})B_{2n}$$

$$= 2nE_{2n-1}(0),$$

where $B_n$ is a Bernoulli Number and $E_n(x)$ is an Euler Polynomial. The first few Genocchi numbers for $n$ Even are $-1$, 1, $-3$, 17, $-155$, 2073, ... (Sloane's A001469).

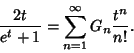
See also Bernoulli Number, Euler Polynomial

References

Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 49, 1974.

Kreweras, G. ``An Additive Generation for the Genocchi Numbers and Two of its Enumerative Meanings.'' Bull. Inst. Combin. Appl. 20, 99-103, 1997.

Kreweras, G. ``Sur les permutations comptées par les nombres de Genocchi de 1-ière et 2-ième espèce.'' Europ. J. Comb. 18, 49-58, 1997.

Sloane, N. J. A. Sequence A001469/M3041 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.