|
|
|
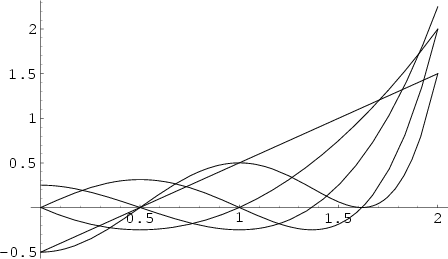
A Polynomial ![]() given by the sum
given by the sum
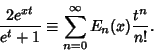 |
(1) |
![$\displaystyle {2^n\over n} \left[{B_n\left({x+1\over 2}\right)-B_n\left({x\over 2}\right)}\right]$](e_2339.gif) |
(2) | ||
| (3) | |||
![$\displaystyle 2{n\choose 2}^{-1} \sum_{k=0}^{n-2} {n\choose k}[(2^{n-k}-1)B_{n-k}B_k(x)],$](e_2342.gif) |
|||
| (4) |
| (5) |
![\begin{displaymath}
E_n(0)=2^{-n}\sum_{j=1}^n\left[{(-1)^{j+n+1}j^k\sum_{k=0}^{n-j}{n+1\choose k}}\right].
\end{displaymath}](e_2349.gif) |
(6) |
| (7) |
See also Bernoulli Polynomial, Euler Number, Genocchi Number
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula.''
§23.1 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, 1979.
Spanier, J. and Oldham, K. B. ``The Euler Polynomials
![]() .''
Ch. 20 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 175-181, 1987.
.''
Ch. 20 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 175-181, 1987.
|
|
|
© 1996-9 Eric W. Weisstein