|
|
|
A Polynomial is a mathematical expression involving a series of Powers in one or more variables
multiplied by Coefficients. A Polynomial in one variable with constant
Coefficients is given by
| (1) |
| (2) |
Exchanging the Coefficients of a one-variable Polynomial
end-to-end produces a Polynomial
| (3) |
The following table gives special names given to polynomials of low orders.
| Order | Polynomial Type |
| 1 | Linear Equation |
| 2 | Quadratic Equation |
| 3 | Cubic Equation |
| 4 | Quartic Equation |
| 5 | Quintic Equation |
| 6 | Sextic Equation |
Polynomials of fourth degree may be computed using three multiplications and five additions if a few quantities are calculated first (Press et al. 1989):
|
|
|
|
|
(4) |
| (5) | |||
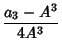 |
(6) | ||
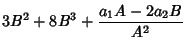 |
(7) | ||
| (8) | |||
| (9) |
Polynomials of orders one to four are solvable using only rational operations and finite root extractions. A first-order
equation is trivially solvable. A second-order equation is soluble using the Quadratic Equation. A third-order equation
is solvable using the Cubic Equation. A fourth-order equation is solvable using the Quartic Equation. It was
proved by Abel ![]() (and Galois
(and Galois ![]() ) using Group Theory that general equations of fifth and higher order
cannot be solved rationally with finite root extractions.
) using Group Theory that general equations of fifth and higher order
cannot be solved rationally with finite root extractions.
However, the general Quintic Equation may be given in terms of the Theta Functions, or
Hypergeometric Functions in one variable. Hermite ![]() and Kronecker
and Kronecker ![]() proved that higher order Polynomials are not soluble in the same manner. Klein showed that the work
of Hermite was implicit in the Group properties of the Icosahedron. Klein's method of solving the
quintic in terms of Hypergeometric Functions in one variable can be extended to the
sextic, but for higher order Polynomials, either Hypergeometric Functions in several variables or ``Siegel functions'' must be used. In the 1880s, Poincaré
proved that higher order Polynomials are not soluble in the same manner. Klein showed that the work
of Hermite was implicit in the Group properties of the Icosahedron. Klein's method of solving the
quintic in terms of Hypergeometric Functions in one variable can be extended to the
sextic, but for higher order Polynomials, either Hypergeometric Functions in several variables or ``Siegel functions'' must be used. In the 1880s, Poincaré ![]() created functions which give the solution to the
created functions which give the solution to the ![]() th order Polynomial equation in finite form. These functions
turned out to be ``natural'' generalizations of the Elliptic Functions.
th order Polynomial equation in finite form. These functions
turned out to be ``natural'' generalizations of the Elliptic Functions.
Given an ![]() th degree Polynomial, the Roots can be found by finding the Eigenvalues
of the Matrix
th degree Polynomial, the Roots can be found by finding the Eigenvalues
of the Matrix
![\begin{displaymath}
\left[{\matrix{
-{a_0/a_n} & -{a_1/a_n} & -{a_2/a_n} & \cdot...
...\vdots & 1 & \ddots & 0\cr
0 & 0 & 0 & \cdots & 0\cr}}\right].
\end{displaymath}](p2_1468.gif) |
(10) |
Polynomial identities involving sums and differences of like Powers include
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) |
| (20) | |||
| (21) | |||
| (22) |
|
|
|
|
|
|
|
|
(23) |
See also Appell Polynomial, Bernstein Polynomial, Bessel Polynomial, Bezout's Theorem, Binomial, Bombieri Inner Product, Bombieri Norm, Chebyshev Polynomial of the First Kind, Chebyshev Polynomial of the Second Kind, Christoffel-Darboux Formula, Christoffel Number, Complex Number, Cyclotomic Polynomial, Descartes' Sign Rule, Discriminant (Polynomial), Durfee Polynomial, Ehrhart Polynomial, Euler Four-Square Identity, Fibonacci Identity, Fundamental Theorem of Algebra, Fundamental Theorem of Symmetric Functions, Gauss-Jacobi Mechanical Quadrature, Gegenbauer Polynomial, Gram-Schmidt Orthonormalization, Greatest Lower Bound, Hermite Polynomial, Hilbert Polynomial, Irreducible Polynomial, Isobaric Polynomial, Isograph, Jensen Polynomial, Kernel Polynomial, Krawtchouk Polynomial, Laguerre Polynomial, Least Upper Bound, Legendre Polynomial, Liouville Polynomial Identity, Lommel Polynomial, Lukács Theorem, Monomial, Orthogonal Polynomials, Perimeter Polynomial, Poisson-Charlier Polynomial, Pollaczek Polynomial, Polynomial Bar Norm, Quarter Squares Rule, Ramanujan 6-10-8 Identity, Root, Runge-Walsh Theorem, Schläfli Polynomial, Separation Theorem, Stieltjes-Wigert Polynomial, Trinomial, Trinomial Identity, Weierstraß's Polynomial Theorem, Zernike Polynomial
References
Barbeau, E. J. Polynomials. New York: Springer-Verlag, 1989.
Bini, D. and Pan, V. Y. Polynomial and Matrix Computations, Vol. 1: Fundamental Algorithms.
Boston, MA: Birkhäuser, 1994.
Borwein, P. and Erdélyi, T. Polynomials and Polynomial Inequalities. New York: Springer-Verlag, 1995.
Cockle, J. ``Notes on the Higher Algebra.'' Quart. J. Pure Applied Math. 4, 49-57, 1861.
Cockle, J. ``Notes on the Higher Algebra (Continued).'' Quart. J. Pure Applied Math. 5, 1-17, 1862.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in C: The Art of Scientific Computing. Cambridge, England: Cambridge University Press, 1989.
Project Mathematics! Polynomials. Videotape (27 minutes). California Institute of
Technology. Available from the Math. Assoc. Amer.
![]() Polynomials
Polynomials
|
|
|
© 1996-9 Eric W. Weisstein