Let 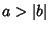 , and write
, and write
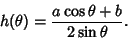 |
(1) |
Then define 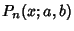 by the Generating Function
by the Generating Function
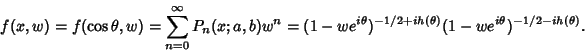 |
(2) |
The Generating Function may also be written
![\begin{displaymath}
f(x,w)=(1-2xw+w^2)^{-1/2}\mathop{\rm exp}\nolimits \left[{(ax+b)\sum_{m=1}^\infty {w^m\over m} U_{m-1}(x)}\right],
\end{displaymath}](p2_1147.gif) |
(3) |
where 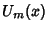 is a Chebyshev Polynomial of the Second Kind. They satisfy the Recurrence Relation
is a Chebyshev Polynomial of the Second Kind. They satisfy the Recurrence Relation
![\begin{displaymath}
nP_n(x;a,b)=[(2n-1+2a)x+2b]P_{n-1}(x;a,b)-(n-1)P_{n-2}(x;a,b)
\end{displaymath}](p2_1149.gif) |
(4) |
for 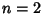 , 3, ...with
, 3, ...with
In terms of the Hypergeometric Function
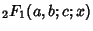 ,
,
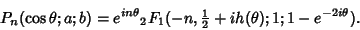 |
(7) |
They obey the orthogonality relation
![\begin{displaymath}
\int_{-1}^1 P_n(x; a,b)P_m(x; a,b)w(x; a,b)\,dx=[n+{\textstyle{1\over 2}}(a+1)]^{-1} \delta_{nm},
\end{displaymath}](p2_1155.gif) |
(8) |
where 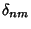 is the Kronecker Delta, for
is the Kronecker Delta, for 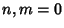 , 1, ..., with the Weight Function
, 1, ..., with the Weight Function
![\begin{displaymath}
w(\cos\theta; a,b)=e^{(2\theta-\pi)h(\theta)} \{\cosh[\pi h(\theta)]\}^{-1}.
\end{displaymath}](p2_1158.gif) |
(9) |
References
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 393-400, 1975.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , and write
, and write
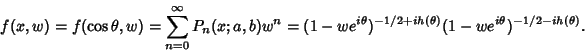
![\begin{displaymath}
f(x,w)=(1-2xw+w^2)^{-1/2}\mathop{\rm exp}\nolimits \left[{(ax+b)\sum_{m=1}^\infty {w^m\over m} U_{m-1}(x)}\right],
\end{displaymath}](p2_1147.gif)