The simplest interpretation of the Kronecker delta is as the discrete version of the Delta Function defined by
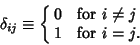 |
(1) |
It has the Complex Generating Function
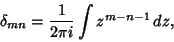 |
(2) |
where 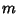 and
and 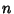 are Integers. In 3-space, the Kronecker delta satisfies the identities
are Integers. In 3-space, the Kronecker delta satisfies the identities
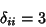 |
(3) |
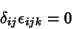 |
(4) |
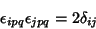 |
(5) |
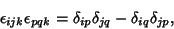 |
(6) |
where Einstein Summation is implicitly assumed, 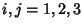 , and
, and 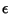 is the Permutation Symbol.
is the Permutation Symbol.
Technically, the Kronecker delta is a Tensor defined by the relationship
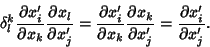 |
(7) |
Since, by definition, the coordinates 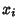 and
and 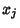 are independent for
are independent for 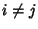 ,
,
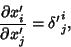 |
(8) |
so
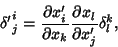 |
(9) |
and 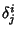 is really a mixed second Rank Tensor. It satisfies
is really a mixed second Rank Tensor. It satisfies
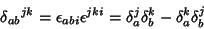 |
(10) |
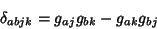 |
(11) |
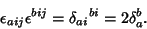 |
(12) |
See also Delta Function, Permutation Symbol
© 1996-9 Eric W. Weisstein
1999-05-26