Defined as the limit of a class of Delta Sequences. Sometimes called the Impulse Symbol.
The most commonly used (equivalent) definitions are
![\begin{displaymath}
\delta(x) \equiv \lim_{n\to \infty} {1\over 2\pi} {\sin[(n+{\textstyle{1\over 2}})x]\over \sin({\textstyle{1\over 2}}x)}
\end{displaymath}](d1_424.gif) |
(1) |
(the so-called Dirichlet Kernel) and
where 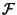 is the Fourier Transform. Some identities include
is the Fourier Transform. Some identities include
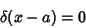 |
(5) |
for 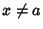 ,
,
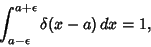 |
(6) |
where 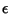 is any Positive number, and
is any Positive number, and
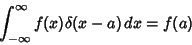 |
(7) |
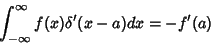 |
(8) |
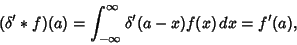 |
(9) |
where 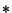 denotes Convolution,
denotes Convolution,
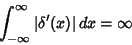 |
(10) |
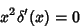 |
(11) |
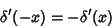 |
(12) |
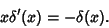 |
(13) |
(13) can be established using Integration by Parts as follows:
Additional identities are
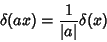 |
(15) |
![\begin{displaymath}
\delta(x^2-a^2)={1\over 2\vert a\vert} [\delta(x+a)+\delta(x-a)]
\end{displaymath}](d1_445.gif) |
(16) |
![\begin{displaymath}
\delta[g(x)] = \sum_i {\delta(x-x_i)\over\vert g'(x_i)\vert},
\end{displaymath}](d1_446.gif) |
(17) |
where the 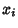 s are the Roots of
s are the Roots of 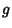 . For example, examine
. For example, examine
![\begin{displaymath}
\delta(x^2+x-2)=\delta[(x-1)(x+2)].
\end{displaymath}](d1_448.gif) |
(18) |
Then 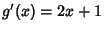 , so
, so
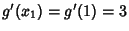 and
and
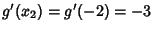 , and we have
, and we have
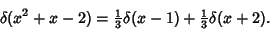 |
(19) |
A Fourier Series expansion of  gives
gives
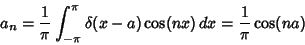 |
(20) |
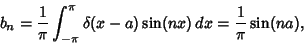 |
(21) |
so
The Fourier Transform of the delta function is
![\begin{displaymath}
{\mathcal F}[\delta(x-x_0)] = \int_{-\infty}^\infty e^{-2\pi ikx}\delta(x-x_0)\,dx = e^{-2\pi ikx_0}.
\end{displaymath}](d1_459.gif) |
(23) |
Delta functions can also be defined in 2-D, so that in 2-D Cartesian Coordinates
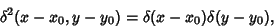 |
(24) |
and in 3-D, so that in 3-D Cartesian Coordinates
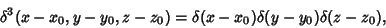 |
(25) |
in Cylindrical Coordinates
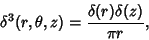 |
(26) |
and in Spherical Coordinates,
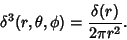 |
(27) |
A series expansion in Cylindrical Coordinates gives
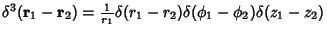
|
|
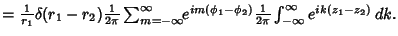
|
|
|
|
(28) |
The delta function also obeys the so-called Sifting Property
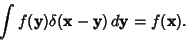 |
(29) |
See also Delta Sequence, Doublet Function, Fourier Transform--Delta Function
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 481-485, 1985.
Spanier, J. and Oldham, K. B. ``The Dirac Delta Function  .''
Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
.''
Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
© 1996-9 Eric W. Weisstein
1999-05-24
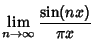
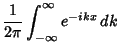
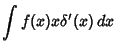
![$\displaystyle -\int \delta(x){d\over dx} [xf(x)]\,dx$](d1_441.gif)
![$\displaystyle -\int \delta[f(x)+xf'(x)]\,dx$](d1_442.gif)
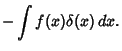
![\begin{displaymath}
\delta[g(x)] = \sum_i {\delta(x-x_i)\over\vert g'(x_i)\vert},
\end{displaymath}](d1_446.gif)
![]() gives
gives
![$\displaystyle {1\over 2\pi} + {1\over \pi} \sum_{n=1}^\infty [\cos(na)\cos(nx)+\sin(na)\sin(nx)]$](d1_457.gif)
![$\displaystyle {1\over 2\pi} + {1\over \pi} \sum_{n=1}^\infty \cos[n(x-a)].$](d1_458.gif)
![]() .''
Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.
.''
Ch. 10 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 79-82, 1987.