|
|
|
The Fourier transform is a generalization of the Complex Fourier Series in the limit as
![]() . Replace the discrete
. Replace the discrete ![]() with the continuous
with the continuous ![]() while letting
while letting ![]() . Then change the sum to
an Integral, and the equations become
. Then change the sum to
an Integral, and the equations become
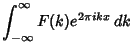 |
(1) | ||
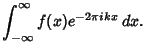 |
(2) |
| (3) |
| (4) |
![$\displaystyle {\mathcal F}[h(t)] = \int_{-\infty}^\infty h(t)e^{-i\omega t}\,dt$](f_1764.gif) |
(5) | ||
![$\displaystyle {\mathcal F}^{-1}[H(\nu)] = {1\over 2\pi}\int_{-\infty}^\infty H(\nu)e^{i\omega t}\,d\omega.$](f_1766.gif) |
(6) |
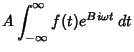 |
(7) | ||
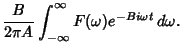 |
(8) |
Since any function can be split up into Even and Odd portions ![]() and
and
![]() ,
,
| (9) |
| (10) |
A function ![]() has a forward and inverse Fourier transform such that
has a forward and inverse Fourier transform such that
![\begin{displaymath}
f(x)=\cases{
\int_{-\infty}^\infty e^{2\pi ikx}\left[{\int_...
...]\cr
\quad {\rm for\ } f(x) {\rm\ discontinuous\ at\ } x,\cr}
\end{displaymath}](f_1779.gif) |
(11) |
The Fourier transform is linear, since if ![]() and
and ![]() have Fourier Transforms
have Fourier Transforms ![]() and
and ![]() , then
, then
|
|
|
|
|
(12) |
| (13) |
The Fourier transform is also symmetric since
![]() implies
implies
![]() .
.
Let ![]() denote the Convolution, then the transforms of convolutions of functions have particularly
nice transforms,
denote the Convolution, then the transforms of convolutions of functions have particularly
nice transforms,
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
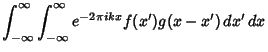 |
|||
![$\displaystyle \int_{-\infty}^\infty \int_{-\infty}^\infty [e^{-2\pi ikx'}f(x')\,dx'][e^{-2\pi ik(x-x')}g(x-x')\,dx]$](f_1799.gif) |
|||
![$\displaystyle \left[{\int_{-\infty}^\infty e^{-2\pi ikx'}f(x')\,dx'}\right]\left[{\int_{-\infty}^\infty e^{-2\pi ikx''}g(x'')\,dx''}\right]$](f_1800.gif) |
|||
| (18) |
There is also a somewhat surprising and extremely important relationship between the Autocorrelation and the Fourier
transform known as the Wiener-Khintchine Theorem. Let
![]() , and
, and ![]() denote the Complex
Conjugate of
denote the Complex
Conjugate of ![]() , then the Fourier Transform of the Absolute Square of
, then the Fourier Transform of the Absolute Square of ![]() is given by
is given by
| (19) |
The Fourier transform of a Derivative ![]() of a function
of a function ![]() is simply related to the transform of the
function
is simply related to the transform of the
function ![]() itself. Consider
itself. Consider
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
The important Modulation Theorem of Fourier transforms allows
![]() to be expressed in terms
of
to be expressed in terms
of
![]() as follows,
as follows,
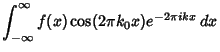 |
|||
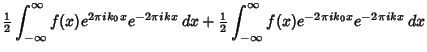 |
|||
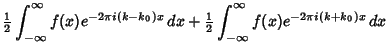 |
|||
| (28) |
Since the Derivative of the Fourier Transform is given by
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
If ![]() has the Fourier Transform
has the Fourier Transform ![]() , then the Fourier transform has the shift property
, then the Fourier transform has the shift property
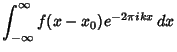 |
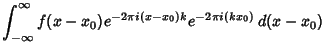 |
||
| (34) |
| (35) |
If ![]() has a Fourier Transform
has a Fourier Transform ![]() , then the Fourier transform obeys a similarity theorem.
, then the Fourier transform obeys a similarity theorem.
| (36) |
The ``equivalent width'' of a Fourier transform is
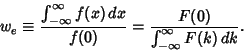 |
(37) |
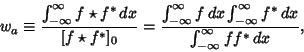 |
(38) |
Any operation on ![]() which leaves its Area unchanged leaves
which leaves its Area unchanged leaves ![]() unchanged, since
unchanged, since
| (39) |
In 2-D, the Fourier transform becomes
| (40) |
| (41) |
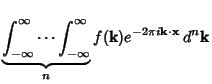 |
(42) | ||
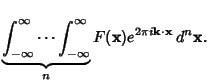 |
(43) |
See also Autocorrelation, Convolution, Discrete Fourier Transform, Fast Fourier Transform, Fourier Series, Fourier-Stieltjes Transform, Hankel Transform, Hartley Transform, Integral Transform, Laplace Transform, Structure Factor, Winograd Transform
References
Arfken, G. ``Development of the Fourier Integral,'' ``Fourier Transforms--Inversion Theorem,'' and
``Fourier Transform of Derivatives.'' §15.2-15.4 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 794-810, 1985.
Blackman, R. B. and Tukey, J. W. The Measurement of Power Spectra, From the Point of View of Communications Engineering.
New York: Dover, 1959.
Bracewell, R. The Fourier Transform and Its Applications. New York: McGraw-Hill, 1965.
Brigham, E. O. The Fast Fourier Transform and Applications. Englewood Cliffs, NJ: Prentice Hall, 1988.
James, J. F. A Student's Guide to Fourier Transforms with Applications in Physics and Engineering.
New York: Cambridge University Press, 1995.
Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988.
Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994.
Morse, P. M. and Feshbach, H. ``Fourier Transforms.'' §4.8 in
Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 453-471, 1953.
Papoulis, A. The Fourier Integral and Its Applications. New York: McGraw-Hill, 1962.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in C: The Art of Scientific Computing. Cambridge, England: Cambridge University Press, 1989.
Sansone, G. ``The Fourier Transform.'' §2.13 in Orthogonal Functions, rev. English ed.
New York: Dover, pp. 158-168, 1991.
Sneddon, I. N. Fourier Transforms. New York: Dover, 1995.
Sogge, C. D. Fourier Integrals in Classical Analysis. New York: Cambridge University Press, 1993.
Spiegel, M. R. Theory and Problems of Fourier Analysis with Applications to Boundary Value Problems.
New York: McGraw-Hill, 1974.
Strichartz, R. Fourier Transforms and Distribution Theory. Boca Raton, FL: CRC Press, 1993.
Titchmarsh, E. C. Introduction to the Theory of Fourier Integrals, 3rd ed. Oxford, England: Clarendon Press, 1948.
Tolstov, G. P. Fourier Series. New York: Dover, 1976.
Walker, J. S. Fast Fourier Transforms, 2nd ed. Boca Raton, FL: CRC Press, 1996.
![]() Fourier Transforms
Fourier Transforms
|
|
|
© 1996-9 Eric W. Weisstein