|
|
|
The Fourier Transform is defined as
| (1) |
| (2) |
![\begin{displaymath}
{\mathcal F}[f(t)] =\sum_{k=0}^{N-1} f_ke^{-2\pi i(n/N\Delta)k\Delta}\Delta
= \Delta\sum_{k=0}^{N-1} f_k e^{-2\pi i nk/N},
\end{displaymath}](d2_604.gif) |
(3) |
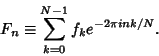 |
(4) |
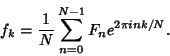 |
(5) |
| (6) |
The discrete Fourier transform is a special case of the z-Transform.
See also Fast Fourier Transform, Fourier Transform, Hartley Transform, Winograd Transform, z-Transform
References
Arfken, G. ``Discrete Orthogonality--Discrete Fourier Transform.'' §14.6 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 787-792, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Fourier Transform of Discretely Sampled
Data.'' §12.1 in Numerical Recipes in C: The Art of Scientific Computing.
Cambridge, England: Cambridge University Press, pp. 494-498, 1989.
|
|
|
© 1996-9 Eric W. Weisstein