A function 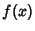 satisfies the Lipschitz condition of order
satisfies the Lipschitz condition of order 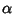 at
at 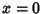 if
if
for all
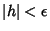 , where
, where 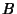 and
and 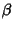 are independent of
are independent of 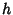 ,
, 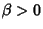 , and
, and 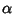 is an Upper Bound
for all
is an Upper Bound
for all 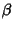 for which a finite
for which a finite 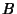 exists.
exists.
See also Hillam's Theorem, Lipschitz Function
© 1996-9 Eric W. Weisstein
1999-05-25
![]() satisfies the Lipschitz condition of order
satisfies the Lipschitz condition of order ![]() at
at ![]() if
if