|
|
|
Fourier series are expansions of Periodic Functions ![]() in terms of an infinite sum of
Sines and Cosines
in terms of an infinite sum of
Sines and Cosines
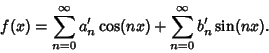 |
(1) |
To compute a Fourier series, use the integral identities
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
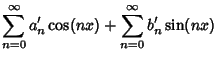 |
|||
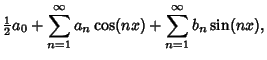 |
(7) |
|
|
|
|
|
|
|
|
|
|
|
(8) |
|
|
|
|
|
|
|
|
|
|
|
(9) |
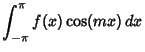 |
![$\displaystyle \int_{-\pi}^\pi\left[{\sum_{n=1}^\infty a_n\cos(nx) + \sum_{n=1}^\infty b_n\sin(nx)+ {\textstyle{1\over 2}}a_0}\right]\cos(mx)\,dx$](f_1667.gif) |
||
![$\displaystyle \sum_{n=1}^\infty \int_{-\pi}^\pi [a_n\cos(nx)\cos(mx)+b_n\sin(nx)\cos(mx)]\,dx+{\textstyle{1\over 2}}a_0 \int_{-\pi}^\pi \cos(mx)\,dx$](f_1668.gif) |
|||
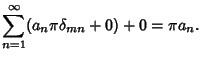 |
(10) |
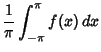 |
(11) | ||
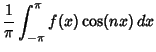 |
(12) | ||
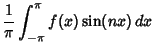 |
(13) |
![\begin{displaymath}
\bar f \equiv \cases{
{\textstyle{1\over 2}}\left[{\lim_{x\...
...to \pi_-} f(x)}\right]\cr
\quad{\rm for\ } x_0 = -\pi, \pi\cr}
\end{displaymath}](f_1674.gif) |
(14) |
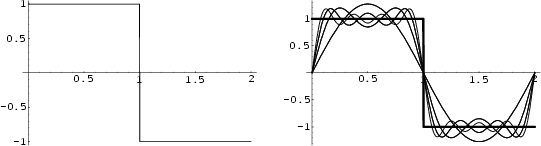
Near points of discontinuity, a ``ringing'' known as the Gibbs Phenomenon, illustrated above, occurs.
For a function ![]() periodic on an interval
periodic on an interval ![]() , use a change of variables to transform the interval of integration
to
, use a change of variables to transform the interval of integration
to ![]() . Let
. Let
| (15) | |||
| (16) |
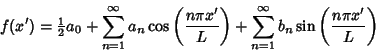 |
(17) |
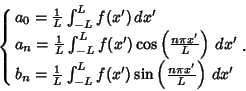 |
(18) |
Because the Sines and Cosines form a Complete Orthogonal Basis, the Superposition Principle holds, and the Fourier series of a linear combination of two functions is the same as the linear combination of the corresponding two series. The Coefficients for Fourier series expansions for a few common functions are given in Beyer (1987, pp. 411-412) and Byerly (1959, p. 51).
The notion of a Fourier series can also be extended to Complex Coefficients.
Consider a real-valued function ![]() . Write
. Write
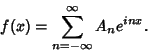 |
(19) |
|
|
|
|
|
|
|
|
|
|
|
(20) |
| (21) |
![$\displaystyle {1\over 2\pi} \int_{-\pi}^\pi f(x)[\cos (nx)-i\sin (nx)]\,dx$](f_1697.gif) |
|||
![$\displaystyle \left\{\begin{array}{ll} {1\over 2\pi}\int_{-\pi}^\pi f(x)[\cos(n...
...i}\int_{-\pi}^\pi f(x)[\cos(nx)-i\sin(nx)]\,dx & \mbox{$n>0$}\end{array}\right.$](f_1698.gif) |
|||
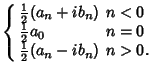 |
(22) |
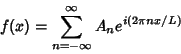 |
(23) |
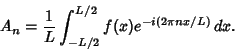 |
(24) |
See also Dirichlet Fourier Series Conditions, Fourier Cosine Series, Fourier Sine Series, Fourier Transform, Gibbs Phenomenon, Lebesgue Constants (Fourier Series), Legendre Series, Riesz-Fischer Theorem
References
Arfken, G. ``Fourier Series.'' Ch. 14 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 760-793, 1985.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics,
with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Carslaw, H. S. Introduction to the Theory of Fourier's Series and Integrals, 3rd ed., rev. and enl.
New York: Dover, 1950.
Davis, H. F. Fourier Series and Orthogonal Functions. New York: Dover, 1963.
Dym, H. and McKean, H. P. Fourier Series and Integrals. New York: Academic Press, 1972.
Folland, G. B. Fourier Analysis and Its Applications. Pacific Grove, CA: Brooks/Cole, 1992.
Groemer, H. Geometric Applications of Fourier Series and Spherical Harmonics.
New York: Cambridge University Press, 1996.
Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988.
Körner, T. W. Exercises for Fourier Analysis. New York: Cambridge University Press, 1993.
Lighthill, M. J. Introduction to Fourier Analysis and Generalised Functions.
Cambridge, England: Cambridge University Press, 1958.
Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994.
Sansone, G. ``Expansions in Fourier Series.'' Ch. 2 in Orthogonal Functions, rev. English ed.
New York: Dover, pp. 39-168, 1991.
![]() Fourier Transforms
Fourier Transforms
|
|
|
© 1996-9 Eric W. Weisstein