|
|
|
Because the Legendre Functions of the First Kind form a
Complete Orthogonal Basis, any Function may be expanded in terms of them
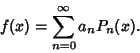 |
(1) |
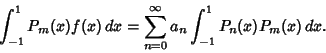 |
(2) |
| (3) |
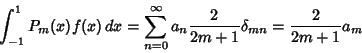 |
(4) |
| (5) |
See also Fourier Series, Jackson's Theorem, Legendre Polynomial, Maclaurin Series, Picone's Theorem, Taylor Series