|
|
|
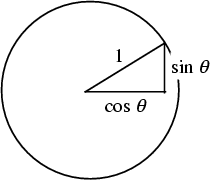
Let ![]() be an Angle measured counterclockwise from the
be an Angle measured counterclockwise from the ![]() -axis along the arc of the unit Circle. Then
-axis along the arc of the unit Circle. Then
![]() is the horizontal coordinate of the arc endpoint. As a result of this definition, the cosine function is
periodic with period
is the horizontal coordinate of the arc endpoint. As a result of this definition, the cosine function is
periodic with period ![]() .
.

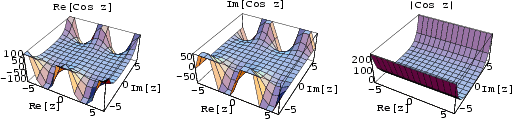
The cosine function has a Fixed Point at 0.739085.

The cosine function can be defined algebraically using the infinite sum
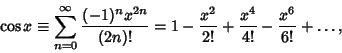 |
(1) |
![\begin{displaymath}
\cos x = \prod_{n=1}^\infty \left[{1 - {4x^2\over\pi^2(2n-1)^2}}\right].
\end{displaymath}](c3_462.gif) |
(2) |
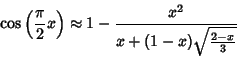 |
(3) |
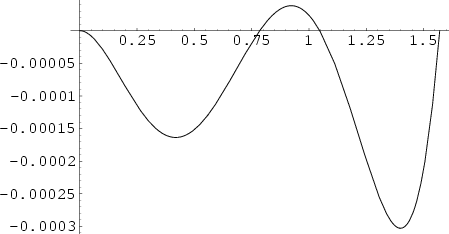
The Fourier Transform of
![]() is given by
is given by
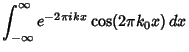 |
|||
| (4) |
The cosine sum rule gives an expansion of the Cosine function of a multiple Angle in terms of a sum of Powers of sines and cosines,
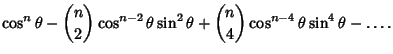 |
(5) |
![\begin{displaymath}
\sum_{n=0}^{N-1} \cos(nx) = \Re\left[{\,\sum_{n=0}^{N-1} e^{inx}}\right].
\end{displaymath}](c3_478.gif) |
(6) |
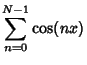 |
![$\displaystyle \Re\left[{{\sin({\textstyle{1\over 2}}Nx)\over\sin({\textstyle{1\over 2}}x)} e^{i(N-1)x/2}}\right]$](c3_480.gif) |
||
![$\displaystyle {\sin({\textstyle{1\over 2}}Nx)\over\sin({\textstyle{1\over 2}}x)} \cos[{\textstyle{1\over 2}}x(N-1)].$](c3_481.gif) |
(7) |
![\begin{displaymath}
\sum_{n=0}^\infty p^n \cos(nx) = \Re\left[{\,\sum_{n=0}^\infty p^ne^{inx}}\right],
\end{displaymath}](c3_482.gif) |
(8) |
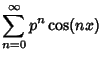 |
![$\displaystyle \Re\left[{1-pe^{-ix}\over 1-2p\cos x+p^2}\right]$](c3_485.gif) |
||
| (9) |
Cvijovic and Klinowski (1995) note that the following series
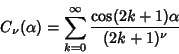 |
(10) |
| (11) |
See also Euler Polynomial, Exponential Sum Formulas, Fourier Transform--Cosine, Hyperbolic Cosine, Sine, Tangent, Trigonometric Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Circular Functions.'' §4.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 71-79, 1972.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 68,
1959.
Cvijovic, D. and Klinowski, J. ``Closed-Form Summation of Some Trigonometric Series.'' Math. Comput. 64, 205-210, 1995.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Project Mathematics! Sines and Cosines, Parts I-III. Videotapes (28, 30, and 30 minutes). California Institute of
Technology. Available from the Math. Assoc. Amer.
Spanier, J. and Oldham, K. B. ``The Sine
![]() and Cosine
and Cosine ![]() Functions.''
Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Functions.''
Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
|
|
|
© 1996-9 Eric W. Weisstein