|
|
|
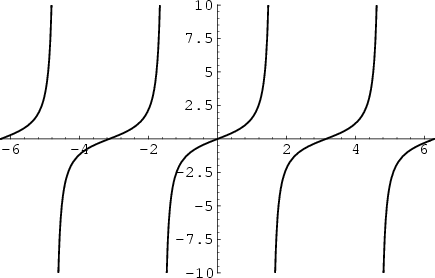
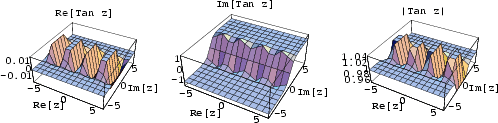
The tangent function is defined by
| (1) |
The Maclaurin Series for the tangent function is
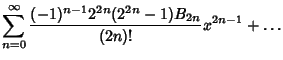 |
|||
| (2) |
![]() is Irrational for any Rational
is Irrational for any Rational ![]() , which can be
proved by writing
, which can be
proved by writing ![]() as a Continued Fraction
as a Continued Fraction
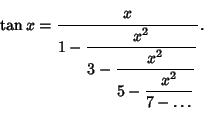 |
(3) |
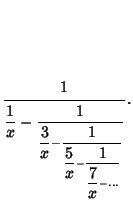 |
(4) |
An interesting identity involving the Product of tangents is
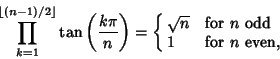 |
(5) |
| (6) |
See also Alternating Permutation, Cosine, Cotangent, Inverse Tangent, Morrie's Law, Sine, Tangent Line, Tangent Plane
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Circular Functions.'' §4.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 71-79, 1972.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Spanier, J. and Oldham, K. B. ``The Tangent
![]() and Cotangent
and Cotangent ![]() Functions.''
Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.
Functions.''
Ch. 34 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 319-330, 1987.
|
|
|
© 1996-9 Eric W. Weisstein