|
|
|
An arrangement of the elements ![]() , ...,
, ..., ![]() such that no element
such that no element ![]() has a magnitude between
has a magnitude between ![]() and
and
![]() is called an alternating (or Zigzag) permutation. The determination of the number
of alternating permutations for the set of the first
is called an alternating (or Zigzag) permutation. The determination of the number
of alternating permutations for the set of the first ![]() Integers
Integers
![]() is known as
André's Problem. An example of an alternating permutation is (1, 3, 2, 5, 4).
is known as
André's Problem. An example of an alternating permutation is (1, 3, 2, 5, 4).
As many alternating permutations among ![]() elements begin by rising as by falling. The magnitude of the
elements begin by rising as by falling. The magnitude of the
![]() s does not matter; only the number of them. Let the number of alternating permutations be given by
s does not matter; only the number of them. Let the number of alternating permutations be given by ![]() . This
quantity can then be computed from
. This
quantity can then be computed from
| (1) |
| (2) |
| (3) |
Curiously enough, the Secant and Tangent Maclaurin Series can be written in terms of the ![]() s as
s as
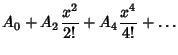 |
(4) | ||
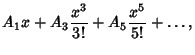 |
(5) |
| (6) |
See also Entringer Number, Euler Number, Euler Zigzag Number, Secant Number, Seidel-Entringer-Arnold Triangle, Tangent Number
References
André, D. ``Developments de
André, D. ``Memoire sur les permutations alternées.'' J. Math. 7, 167-184, 1881.
Arnold, V. I. ``Bernoulli-Euler Updown Numbers Associated with Function Singularities, Their Combinatorics
and Arithmetics.'' Duke Math. J. 63, 537-555, 1991.
Arnold, V. I. ``Snake Calculus and Combinatorics of Bernoulli, Euler, and Springer Numbers for Coxeter Groups.''
Russian Math. Surveys 47, 3-45, 1992.
Bauslaugh, B. and Ruskey, F. ``Generating Alternating Permutations Lexicographically.'' BIT 30, 17-26, 1990.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 110-111, 1996.
Dörrie, H. ``André's Deviation of the Secant and Tangent Series.'' §16 in
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 64-69, 1965.
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 69-75, 1985.
Knuth, D. E. and Buckholtz, T. J. ``Computation of Tangent, Euler, and Bernoulli Numbers.'' Math. Comput. 21, 663-688, 1967.
Millar, J.; Sloane, N. J. A.; and Young, N. E. ``A New Operation on Sequences: The Boustrophedon Transform.''
J. Combin. Th. Ser. A 76, 44-54, 1996.
Ruskey, F. ``Information of Alternating Permutations.''
http://sue.csc.uvic.ca/~cos/inf/perm/Alternating.html.
Sloane, N. J. A. Sequence
A000111/M1492
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() et
et ![]() .'' C. R. Acad. Sci. Paris 88, 965-967, 1879.
.'' C. R. Acad. Sci. Paris 88, 965-967, 1879.
|
|
|
© 1996-9 Eric W. Weisstein