Euclid  defined a line as a ``breadthless length,'' and a straight line as a line which ``lies evenly with the
points on itself'' (Kline 1956, Dunham 1990). Lines are intrinsically 1-dimensional objects, but may be embedded in higher dimensional
Spaces. An infinite line passing through points
defined a line as a ``breadthless length,'' and a straight line as a line which ``lies evenly with the
points on itself'' (Kline 1956, Dunham 1990). Lines are intrinsically 1-dimensional objects, but may be embedded in higher dimensional
Spaces. An infinite line passing through points 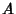 and
and 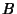 is denoted
is denoted
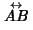 . A Line Segment terminating at these points is denoted
. A Line Segment terminating at these points is denoted 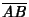 .
A line is sometimes called a Straight Line or, more archaically, a Right Line (Casey 1893), to emphasize that
it has no curves anywhere along its length.
.
A line is sometimes called a Straight Line or, more archaically, a Right Line (Casey 1893), to emphasize that
it has no curves anywhere along its length.
Consider first lines in a 2-D Plane. The line with x-Intercept 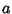 and
y-Intercept
and
y-Intercept 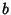 is given by
the intercept form
is given by
the intercept form
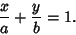 |
(1) |
The line through 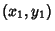 with Slope
with Slope 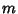 is given by the point-slope form
is given by the point-slope form
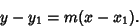 |
(2) |
The line with 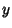 -intercept
-intercept 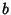 and slope
and slope 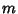 is given by the slope-intercept form
is given by the slope-intercept form
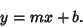 |
(3) |
The line through 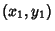 and
and 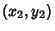 is given by the two point form
is given by the two point form
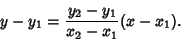 |
(4) |
Other forms are
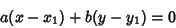 |
(5) |
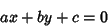 |
(6) |
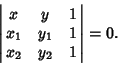 |
(7) |
A line in 2-D can also be represented as a Vector. The Vector along the line
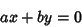 |
(8) |
is given by
![\begin{displaymath}
t\left[{\matrix{-b\cr a\cr}}\right],
\end{displaymath}](l2_181.gif) |
(9) |
where 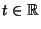 . Similarly, Vectors of the form
. Similarly, Vectors of the form
![\begin{displaymath}
t\left[{\matrix{a\cr b\cr}}\right]
\end{displaymath}](l2_183.gif) |
(10) |
are Perpendicular to the line. Three points lie on a line if
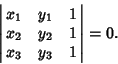 |
(11) |
The Angle between lines
is
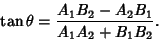 |
(14) |
The line joining points with Trilinear Coordinates
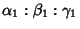 and
and
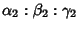 is the set of point
is the set of point
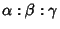 satisfying
satisfying
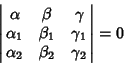 |
(15) |
 |
(16) |
Three lines Concur if their Trilinear Coordinates satisfy
in which case the point is
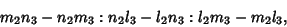 |
(20) |
or if the Coefficients of the lines
satisfy
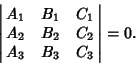 |
(24) |
Two lines Concur if their Trilinear Coordinates satisfy
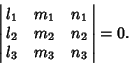 |
(25) |
The line through 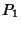 is the direction
is the direction 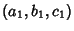 and the line through
and the line through 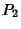 in direction
in direction 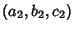 intersect Iff
intersect Iff
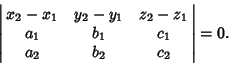 |
(26) |
The line through a point
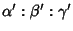 Parallel to
Parallel to
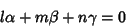 |
(27) |
is
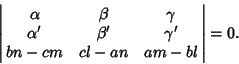 |
(28) |
The lines
are Parallel if
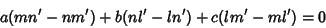 |
(31) |
for all 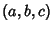 , and Perpendicular if
, and Perpendicular if
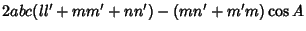
|
|
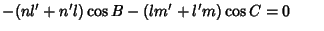
|
(32) |
for all 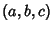 (Sommerville 1924). The line through a point
(Sommerville 1924). The line through a point
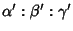 Perpendicular to
(32) is given by
Perpendicular to
(32) is given by
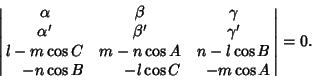 |
(33) |
In 3-D Space, the line passing through the point 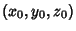 and Parallel to the Nonzero Vector
and Parallel to the Nonzero Vector
![\begin{displaymath}
{\bf v}=\left[{\matrix{a\cr b\cr c\cr}}\right]
\end{displaymath}](l2_218.gif) |
(34) |
has parametric equations
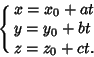 |
(35) |
See also Asymptote, Brocard Line, Collinear, Concur, Critical Line, Desargues'
Theorem, Erdös-Anning Theorem, Line Segment, Ordinary Line, Pencil,
Point, Point-Line Distance--2-D, Point-Line Distance--3-D, Plane, Range (Line Segment), Ray, Solomon's Seal Lines, Steiner Set,
Steiner's Theorem, Sylvester's Line Problem
References
Casey, J. ``The Right Line.'' Ch. 2 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 30-95, 1893.
Dunham, W. Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 32, 1990.
Kline, M. ``The Straight Line.'' Sci. Amer. 156, 105-114, Mar. 1956.
MacTutor History of Mathematics Archive. ``Straight Line.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Straight.html.
Sommerville, D. M. Y. Analytical Conics. London: G. Bell, p. 186, 1924.
Spanier, J. and Oldham, K. B. ``The Linear Function 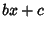 and Its Reciprocal.''
Ch. 7 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 53-62, 1987.
and Its Reciprocal.''
Ch. 7 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 53-62, 1987.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() defined a line as a ``breadthless length,'' and a straight line as a line which ``lies evenly with the
points on itself'' (Kline 1956, Dunham 1990). Lines are intrinsically 1-dimensional objects, but may be embedded in higher dimensional
Spaces. An infinite line passing through points
defined a line as a ``breadthless length,'' and a straight line as a line which ``lies evenly with the
points on itself'' (Kline 1956, Dunham 1990). Lines are intrinsically 1-dimensional objects, but may be embedded in higher dimensional
Spaces. An infinite line passing through points ![]() and
and ![]() is denoted
is denoted
![]() . A Line Segment terminating at these points is denoted
. A Line Segment terminating at these points is denoted ![]() .
A line is sometimes called a Straight Line or, more archaically, a Right Line (Casey 1893), to emphasize that
it has no curves anywhere along its length.
.
A line is sometimes called a Straight Line or, more archaically, a Right Line (Casey 1893), to emphasize that
it has no curves anywhere along its length.
![]() and
y-Intercept
and
y-Intercept ![]() is given by
the intercept form
is given by
the intercept form
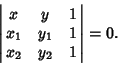
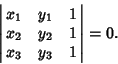
![]() and
and
![]() is the set of point
is the set of point
![]() satisfying
satisfying
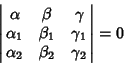
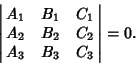
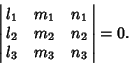
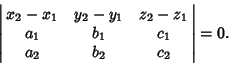
![]() Parallel to
Parallel to
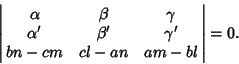
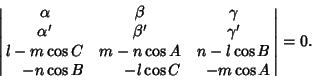
![]() and Parallel to the Nonzero Vector
and Parallel to the Nonzero Vector
![\begin{displaymath}
{\bf v}=\left[{\matrix{a\cr b\cr c\cr}}\right]
\end{displaymath}](l2_218.gif)
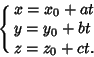
![]() and Its Reciprocal.''
Ch. 7 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 53-62, 1987.
and Its Reciprocal.''
Ch. 7 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 53-62, 1987.