Given a line 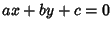 and a point
and a point 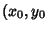 ), in slope-intercept form, the equation
of the line is
), in slope-intercept form, the equation
of the line is
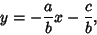 |
(1) |
so the line has Slope 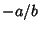 . Points on the line have the vector coordinates
. Points on the line have the vector coordinates
![\begin{displaymath}
\left[{\matrix{x\cr -{a\over b}x-{c\over d}\cr}}\right] = \l...
...r d}\cr}}\right]-{1\over b}\left[{\matrix{-b\cr a\cr}}\right].
\end{displaymath}](p2_770.gif) |
(2) |
Therefore, the Vector
![\begin{displaymath}
\left[{\matrix{-b\cr a\cr}}\right]
\end{displaymath}](p2_771.gif) |
(3) |
is Parallel to the line, and the Vector
![\begin{displaymath}
{\bf v} =\left[{\matrix{a\cr b\cr}}\right]
\end{displaymath}](p2_772.gif) |
(4) |
is Perpendicular to it. Now, a Vector from the point to the line is given by
![\begin{displaymath}
{\bf r} = \left[{\matrix{x-x_0\cr y-y_0\cr}}\right].
\end{displaymath}](p2_773.gif) |
(5) |
Projecting 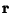 onto
onto 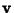 ,
,
If the line is represented by the endpoints of a Vector 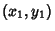 and
and 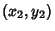 , then the Perpendicular
Vector is
, then the Perpendicular
Vector is
![\begin{displaymath}
\bf v= \left[{\matrix{y_2-y_1\cr -(x_2-x_1)\cr}}\right]
\end{displaymath}](p2_782.gif) |
(7) |
![\begin{displaymath}
\hat{\bf v}= {1\over s}\left[{\matrix{y_2-y_1\cr -(x_2-x_1)\cr}}\right],
\end{displaymath}](p2_783.gif) |
(8) |
where
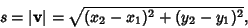 |
(9) |
so the distance is
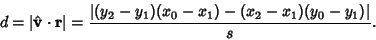 |
(10) |
The distance from a point (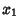 ,
,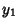 ) to the line
) to the line 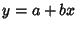 can be computed using Vector algebra. Let
can be computed using Vector algebra. Let  be a Vector in the same direction as the line
be a Vector in the same direction as the line
A given point on the line is
![\begin{displaymath}
{\bf x}=\left[{\matrix{x_1\cr y_1\cr}}\right]-\left[{\matrix{0\cr -a\cr}}\right] = \left[{\matrix{x_1\cr y_1-a\cr}}\right],
\end{displaymath}](p2_794.gif) |
(13) |
so the point-line distance is
Therefore,
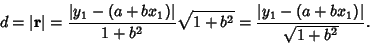 |
(15) |
This result can also be obtained much more simply by noting that the Perpendicular distance is just 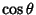 times the vertical distance
times the vertical distance
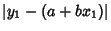 . But the Slope
. But the Slope 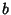 is just
is just 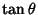 , so
, so
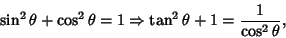 |
(16) |
and
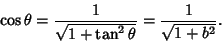 |
(17) |
The Perpendicular distance is then
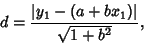 |
(18) |
the same result as before.
See also Line, Point, Point-Line Distance--3-D
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and a point
and a point ![]() ), in slope-intercept form, the equation
of the line is
), in slope-intercept form, the equation
of the line is
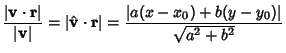
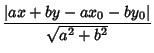
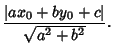
![]() ,
,![]() ) to the line
) to the line ![]() can be computed using Vector algebra. Let
can be computed using Vector algebra. Let ![]() be a Vector in the same direction as the line
be a Vector in the same direction as the line
![$\displaystyle \left[\begin{array}{c}x\\ a+bx\end{array}\right]-\left[\begin{array}{c}0\\ a\end{array}\right]=\left[\begin{array}{c}x\\ bx\end{array}\right]$](p2_791.gif)
![$\displaystyle {1\over \sqrt{b^2+1}} \left[\begin{array}{c}1\\ b\end{array}\right].$](p2_793.gif)
![$\displaystyle {1\over 1+b^2}\left({\left[\begin{array}{c}x_1\\ y_1-a\end{array...
...nd{array}\right] -\left[\begin{array}{c}x_1\\ y_1-a\end{array}\right]\nonumber$](p2_797.gif)
![$\displaystyle {x_1+b(y_1-a)\over 1+b^2}\left[\begin{array}{c}1\\ b\end{array}\right]-\left[\begin{array}{c}x_1\\ y_1-a\end{array}\right]$](p2_798.gif)
![$\displaystyle {1\over 1+b^2}\left[\begin{array}{c}b(y_1-a)-b^2x_1\\ bx_1+b^2y_1-ab^2-y_1+a-b^2y_1+ab^2\end{array}\right]$](p2_799.gif)
![$\displaystyle {1\over 1+b^2} \left[\begin{array}{c}b[(y_1-a)-bx_1]\\ -[(y_1-a)-bx_1]\end{array}\right]$](p2_800.gif)
![$\displaystyle {y_1-(a+bx_1)\over 1+b^2} \left[\begin{array}{c}b\\ -1\end{array}\right].$](p2_801.gif)