|
|
|
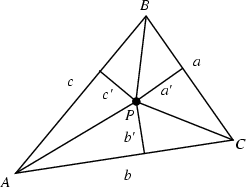
Given a Triangle ![]() , the trilinear coordinates of a point
, the trilinear coordinates of a point ![]() with respect to
with respect to ![]() are an
ordered Triple of numbers, each of which is Proportional to the directed distance from
are an
ordered Triple of numbers, each of which is Proportional to the directed distance from ![]() to one of the
side lines. Trilinear coordinates are denoted
to one of the
side lines. Trilinear coordinates are denoted
![]() or
or
![]() and also are known as
Barycentric Coordinates, Homogeneous Coordinates, or ``trilinears.''
and also are known as
Barycentric Coordinates, Homogeneous Coordinates, or ``trilinears.''
In trilinear coordinates, the three Vertices ![]() ,
, ![]() , and
, and ![]() are given by
are given by ![]() ,
, ![]() , and
, and
![]() . Let the point
. Let the point ![]() in the above diagram have trilinear coordinates
in the above diagram have trilinear coordinates
![]() and lie at distances
and lie at distances
![]() ,
, ![]() , and
, and ![]() from the sides
from the sides ![]() ,
, ![]() , and
, and ![]() , respectively. Then the distances
, respectively. Then the distances ![]() ,
, ![]() ,
and
,
and ![]() can be found by writing
can be found by writing ![]() for the Area of
for the Area of ![]() , and similarly for
, and similarly for
![]() and
and ![]() . We then have
. We then have
| (1) |
| (2) |
Trilinear coordinates are unchanged when each is multiplied by any constant ![]() , so
, so
| (3) |
| (4) |
| (5) |
| (6) |
Trilinear coordinates for some common Points are summarized in the following table,
where ![]() ,
, ![]() , and
, and ![]() are the angles at the corresponding vertices and
are the angles at the corresponding vertices and ![]() ,
, ![]() , and
, and ![]() are the opposite
side lengths.
are the opposite
side lengths.
| Point | Trilinear Center Function |
| Centroid |
|
| Circumcenter |
|
| de Longchamps Point |
|
| Equal Detour Point |
|
| Feuerbach Point |
|
| Incenter |
1 |
| Isoperimetric Point |
|
| Lemoine Point | |
| Nine-Point Center |
|
| Orthocenter |
|
| Vertex |
|
| Vertex |
|
| Vertex |
To convert trilinear coordinates to a vector position for a given triangle specified by the ![]() - and
- and ![]() -coordinates of
its axes, pick two Unit Vectors along the sides. For instance, pick
-coordinates of
its axes, pick two Unit Vectors along the sides. For instance, pick
| (7) | |||
| (8) |
| (9) |
| (10) | |||
| (11) |
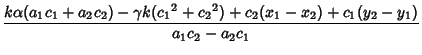 |
(12) | ||
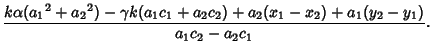 |
(13) |
But ![]() and
and ![]() are Unit Vectors, so
are Unit Vectors, so
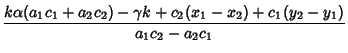 |
(14) | ||
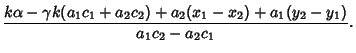 |
(15) |
| (16) |
See also Areal Coordinates, Exact Trilinear Coordinates, Orthocentric Coordinates, Power Curve, Quadriplanar Coordinates, Triangle, Trilinear Polar
References
Boyer, C. B. History of Analytic Geometry. New York: Yeshiva University, 1956.
Casey, J. ``The General Equation--Trilinear Co-Ordinates.'' Ch. 10 in
A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 333-348, 1893.
Coolidge, J. L. A Treatise on Algebraic Plane Curves. New York: Dover, pp. 67-71, 1959.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.
Coxeter, H. S. M. ``Some Applications of Trilinear Coordinates.'' Linear Algebra Appl. 226-228, 375-388, 1995.
Kimberling, C. ``Triangle Centers and Central Triangles.'' Congr. Numer. 129, 1-295, 1998.
|
|
|
© 1996-9 Eric W. Weisstein