|
|
|
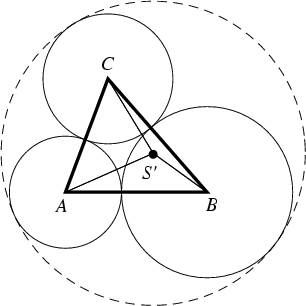
The point ![]() which makes the Perimeters of the Triangles
which makes the Perimeters of the Triangles ![]() ,
, ![]() ,
and
,
and ![]() equal. The isoperimetric point exists Iff the largest Angle of the triangle satisfies
equal. The isoperimetric point exists Iff the largest Angle of the triangle satisfies
See also Equal Detour Point, Perimeter, Soddy Circles
References
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, 163-187, 1994.
Kimberling, C. ``Isoperimetric Point and Equal Detour Point.''
http://cedar.evansville.edu/~ck6/tcenters/recent/isoper.html.
Kimberling, C. and Wagner, R. W. ``Problem E 3020 and Solution.'' Amer. Math. Monthly 93, 650-652, 1986.
Veldkamp, G. R. ``The Isoperimetric Point and the Point(s) of Equal Detour.'' Amer. Math. Monthly 92, 546-558, 1985.