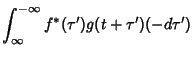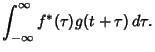Let 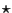 denote cross-correlation. Then the cross-correlation of two functions
denote cross-correlation. Then the cross-correlation of two functions 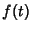 and
and 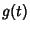 of a real
variable
of a real
variable 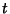 is defined by
is defined by
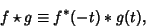 |
(1) |
where 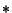 denotes Convolution and
denotes Convolution and 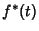 is the Complex Conjugate of
is the Complex Conjugate of 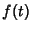 . The
Convolution is defined by
. The
Convolution is defined by
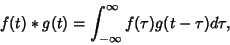 |
(2) |
therefore
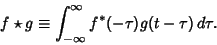 |
(3) |
Let
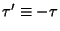 , so
, so 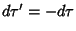 and
and
The cross-correlation satisfies the identity
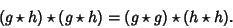 |
(5) |
If 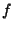 or
or 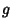 is Even, then
is Even, then
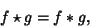 |
(6) |
where 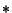 denotes Convolution.
denotes Convolution.
See also Autocorrelation, Convolution, Cross-Correlation Theorem
© 1996-9 Eric W. Weisstein
1999-05-25
![]() denote cross-correlation. Then the cross-correlation of two functions
denote cross-correlation. Then the cross-correlation of two functions ![]() and
and ![]() of a real
variable
of a real
variable ![]() is defined by
is defined by