Cross-Cap

$\begin{figure}\begin{center}\BoxedEPSF{CrossCap.epsf}\end{center}\end{figure}$

The self-intersection of a one-sided Surface. It can be described as a circular Hole which, when entered, exits from its opposite point (from a topological viewpoint, both singular points on the cross-cap are equivalent). The cross-cap has a segment of double points which terminates at two ``Pinch Points'' known as Whitney Singularities.

The cross-cap can be generated using the general method for Nonorientable Surfaces using the polynomial function

$\begin{displaymath} {\bf f}(x,y,z)=(xz, yz, {\textstyle{1\over 2}}(z^2-x^2)) \end{displaymath}$

(1)

(Pinkall 1986). Transforming to Spherical Coordinates gives

$\displaystyle x(u,v)$	$\textstyle =$	$\displaystyle {\textstyle{1\over 2}}\cos u\sin(2v)$	(2)
$\displaystyle y(u,v)$	$\textstyle =$	$\displaystyle {\textstyle{1\over 2}}\sin u\sin(2v)$	(3)
$\displaystyle z(u,v)$	$\textstyle =$	$\displaystyle {\textstyle{1\over 2}}(\cos^2 v-\cos^2 u\sin^2 v)$	(4)

for $u\in [0, 2\pi)$ and $v\in[0,\pi/2]$ . To make the equations slightly simpler, all three equations are normally multiplied by a factor of 2 to clear the arbitrary scaling constant. Three views of the cross-cap generated using this equation are shown above. Note that the middle one looks suspiciously like Maeder's Owl Minimal Surface.

Another representation is

$\begin{displaymath} {\bf f}(x,y,z)=(yz, 2xy, x^2-y^2), \end{displaymath}$

(5)

(Gray 1993), giving parametric equations

$\displaystyle x$	$\textstyle =$	$\displaystyle {\textstyle{1\over 2}}\sin u\sin(2v)$	(6)
$\displaystyle y$	$\textstyle =$	$\displaystyle \sin(2u)\sin^2 v$	(7)
$\displaystyle z$	$\textstyle =$	$\displaystyle \cos(2u)\sin^2 v,$	(8)

(Geometry Center) where, for aesthetic reasons, the

- and

-coordinates have been multiplied by 2 to produce a squashed, but topologically equivalent, surface. Nordstrand gives the implicit equation

$\begin{displaymath} 4x^2(x^2+y^2+z^2+z)+y^2(y^2+z^2-1)=0 \end{displaymath}$

(9)

which can be solved for

to yield

$\begin{displaymath} z={-2x^2\pm\sqrt{(y^2+2x^2)(1-4x^2-y^2)}\over 4x^2+y^2}. \end{displaymath}$

(10)

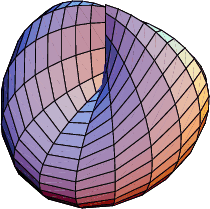
$\begin{figure}\begin{center}\BoxedEPSF{CrossCapCylindroid.epsf}\end{center}\end{figure}$

Taking the inversion of a cross-cap such that (0, 0, ) is sent to $\infty$ gives a Cylindroid, shown above (Pinkall 1986).

The cross-cap is one of the three possible Surfaces obtained by sewing a Möbius Strip to the edge of a Disk. The other two are the Boy Surface and Roman Surface.

References

Fischer, G. (Ed.). Plate 107 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, p. 108, 1986.

Geometry Center. ``The Crosscap.'' http://www.geom.umn.edu/zoo/toptype/pplane/cap/.

Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, p. 64, 1986.