|
|
|
A Nonorientable Surface which is one of the three possible Surfaces obtained by sewing a Möbius Strip to the edge of a Disk. The other two are the Cross-Cap and Roman Surface. The Boy surface is a model of the Projective Plane without singularities and is a Sextic Surface.
The Boy surface can be described using the general method for Nonorientable Surfaces,
but this was not known until the analytic equations were found by Apéry (1986). Based on the fact that
it had been proven impossible to describe the surface using quadratic polynomials, Hopf had conjectured that
quartic polynomials were also insufficient (Pinkall 1986). Apéry's Immersion proved this conjecture wrong,
giving the equations explicitly in terms of the standard form for a Nonorientable Surface,
| (1) | |||
| (2) | |||
| (3) |
Plugging in
| (4) | |||
| (5) | |||
| (6) |
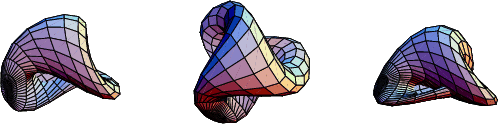
The ![]() parameterization can also be written as
parameterization can also be written as
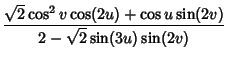 |
(7) | ||
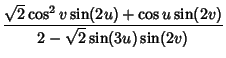 |
(8) | ||
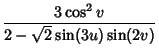 |
(9) |

Three views of the surface obtained using this parameterization are shown above.
In fact, a Homotopy (smooth deformation) between the Roman Surface and Boy surface is given by the
equations
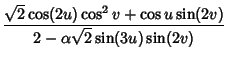 |
(10) | ||
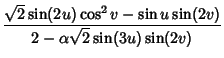 |
(11) | ||
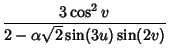 |
(12) |
In ![]() , the parametric representation is
, the parametric representation is
| (13) | |||
| (14) | |||
| (15) | |||
| (16) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(17) |
| (18) | |||
| (19) | |||
| (20) | |||
| (21) |
See also Cross-Cap, Immersion, Möbius Strip, Nonorientable Surface, Real Projective Plane, Roman Surface, Sextic Surface
References
Apéry, F. ``The Boy Surface.'' Adv. Math. 61, 185-266, 1986.
Boy, W. ``Über die Curvatura integra und die Topologie geschlossener Flächen.'' Math. Ann 57, 151-184, 1903.
Brehm, U. ``How to Build Minimal Polyhedral Models of the Boy Surface.'' Math. Intell. 12,
51-56, 1990.
Carter, J. S. ``On Generalizing Boy Surface--Constructing a Generator of the 3rd Stable Stem.''
Trans. Amer. Math. Soc. 298, 103-122, 1986.
Fischer, G. (Ed.). Plates 115-120 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, pp. 110-115, 1986.
Geometry Center. ``Boy's Surface.''
http://www.geom.umn.edu/zoo/toptype/pplane/boy/.
Hilbert, D. and Cohn-Vossen, S. §46-47 in Geometry and the Imagination. New York: Chelsea, 1952.
Nordstrand, T. ``Boy's Surface.''
http://www.uib.no/people/nfytn/boytxt.htm.
Petit, J.-P. and Souriau, J. ``Une représentation analytique de la surface de Boy.''
C. R. Acad. Sci. Paris Sér. 1 Math 293, 269-272, 1981.
Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer).
Braunschweig, Germany: Vieweg, pp. 64-65, 1986.
Stewart, I. Game, Set and Math. New York: Viking Penguin, 1991.
Wang, P. ``Renderings.''
http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/.
|
|
|
© 1996-9 Eric W. Weisstein