A quadratic equation is a second-order Polynomial
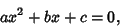 |
(1) |
with 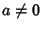 . The roots
. The roots 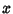 can be found by Completing the Square:
can be found by Completing the Square:
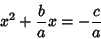 |
(2) |
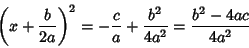 |
(3) |
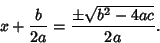 |
(4) |
Solving for 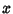 then gives
then gives
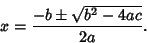 |
(5) |
This is the Quadratic Formula.
An alternate form is given by dividing (1) through by 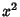 :
:
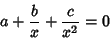 |
(6) |
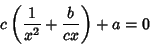 |
(7) |
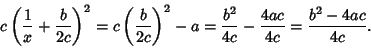 |
(8) |
Therefore,
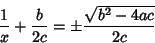 |
(9) |
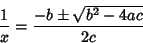 |
(10) |
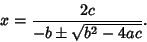 |
(11) |
This form is helpful if 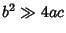 , in which case the usual form of the Quadratic Formula can give inaccurate
numerical results for one of the Roots. This can be avoided by defining
, in which case the usual form of the Quadratic Formula can give inaccurate
numerical results for one of the Roots. This can be avoided by defining
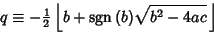 |
(12) |
so that 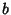 and the term under the Square Root sign always have the same sign.
Now, if
and the term under the Square Root sign always have the same sign.
Now, if 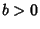 , then
, then
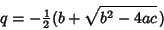 |
(13) |
so
Similarly, if 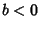 , then
, then
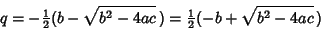 |
(17) |
so
Therefore, the Roots are always given by 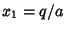 and
and 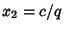 .
.
See also Carlyle Circle, Conic Section, Cubic Equation, Quartic Equation,
Quintic Equation, Sextic Equation
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 17, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 9, 1987.
Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 91-92, 1996.
King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Quadratic and Cubic Equations.'' §5.6 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 178-180, 1992.
Spanier, J. and Oldham, K. B. ``The Quadratic Function 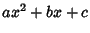 and Its Reciprocal.''
Ch. 16 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 123-131, 1987.
and Its Reciprocal.''
Ch. 16 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 123-131, 1987.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() :
:
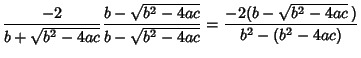
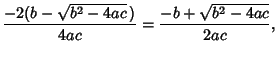
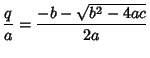
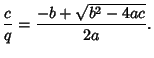
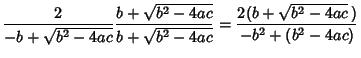
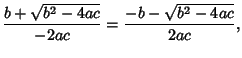
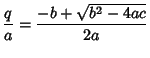
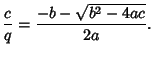
![]() and Its Reciprocal.''
Ch. 16 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 123-131, 1987.
and Its Reciprocal.''
Ch. 16 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 123-131, 1987.