|
|
|
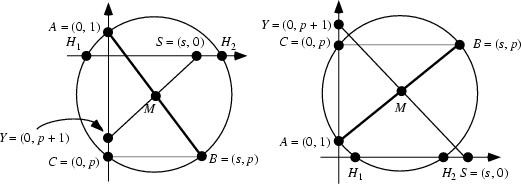
Consider a Quadratic Equation ![]() where
where ![]() and
and ![]() denote signed lengths. The Circle
which has the points
denote signed lengths. The Circle
which has the points ![]() and
and ![]() as a Diameter is then called the Carlyle circle
as a Diameter is then called the Carlyle circle ![]() of the
equation. The Center of
of the
equation. The Center of ![]() is then at the Midpoint of
is then at the Midpoint of ![]() ,
,
![]() , which is also the
Midpoint of
, which is also the
Midpoint of ![]() and
and ![]() . Call the points at which
. Call the points at which ![]() crosses the x-Axis
crosses the x-Axis
![]() and
and ![]() (with
(with ![]() ). Then
). Then
See also 257-gon, 65537-gon, Heptadecagon, Pentagon
References
De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly
98, 97-108, 1991.
Eves, H. An Introduction to the History of Mathematics, 6th ed. Philadelphia, PA: Saunders, 1990.
Leslie, J. Elements of Geometry and Plane Trigonometry with an Appendix and Very Copious Notes and
Illustrations, 4th ed., improved and exp. Edinburgh: W. & G. Tait, 1820.