Heptadecagon

The Regular Polygon of 17 sides is called the Heptadecagon, or sometimes the Heptakaidecagon. Gauß proved in 1796 (when he was 19 years old) that the heptadecagon is Constructible with a Compass and Straightedge. Gauss's proof appears in his monumental work Disquisitiones Arithmeticae. The proof relies on the property of irreducible Polynomial equations that Roots composed of a finite number of Square Root extractions only exist when the order of the equation is a product of the form $2^a3^b F_c\cdot F_d \cdots F_e$, where the $F_n$ are distinct Primes of the form

$$F_n=2^{2^n}+1,$$

known as Fermat Primes. Constructions for the regular Triangle ($3^1$), Square ($2^2$), Pentagon ($2^{2^1}+1$), Hexagon ($2^1 3^1$), etc., had been given by Euclid, but constructions based on the Fermat Primes $\geq 17$ were unknown to the ancients. The first explicit construction of a heptadecagon was given by Erchinger in about 1800.

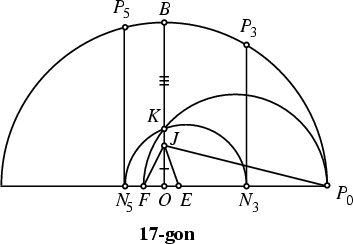
The following elegant construction for the heptadecagon (Yates 1949, Coxeter 1969, Stewart 1977, Wells 1992) was first given by Richmond (1893).

1. Given an arbitrary point $O$, draw a Circle centered on $O$ and a Diameter drawn through $O$.

2. Call the right end of the Diameter dividing the Circle into a Semicircle $P_0$.

3. Construct the Diameter Perpendicular to the original Diameter by finding the Perpendicular Bisector $OB$.

4. Find $J$ a Quarter the way up $OB$.

5. Join $JP_0$ and find $E$ so that $\angle OJE$ is a Quarter of $\angle OJP_0$.

6. Find $F$ so that $\angle EJF$ is 45°.

7. Construct the Semicircle with Diameter $FP_0$.

8. This Semicircle cuts $OB$ at $K$.

9. Draw a Semicircle with center $E$ and Radius $EK$.

10. This cuts the extension of $OP_0$ at $N_3$.

11. Construct a line Perpendicular to $OP_0$ through $N_3$.

12. This line meets the original Semicircle at $P_3$.

13. You now have points $P_0$ and $P_3$ of a heptadecagon.

14. Use $P_0$ and $P_3$ to get the remaining 15 points of the heptadecagon around the original Circle by constructing $P_0$, $P_3$, $P_6$, $P_9$, $P_{12}$, $P_{15}$, $P_1$, $P_4$, $P_7$, $P_{10}$, $P_{13}$, $P_{16}$, $P_2$, $P_5$, $P_8$, $P_{11}$, and $P_{14}$.

15. Connect the adjacent points $P_i$.

This construction, when suitably streamlined, has Simplicity 53. The construction of Smith (1920) has a greater Simplicity of 58. Another construction due to Tietze (1965) and reproduced in Hall (1970) has a Simplicity of 50. However, neither Tietze (1965) nor Hall (1970) provides a proof that this construction is correct. Both Richmond's and Tietze's constructions require extensive calculations to prove their validity. De Temple (1991) gives an elegant construction involving the Carlyle Circles which has Geometrography symbol $8S_1+4S_2+22C_1+11C_3$ and Simplicity 45. The construction problem has now been automated to some extent (Bishop 1978).

See also 257-gon, 65537-gon, Compass, Constructible Polygon, Fermat Number, Fermat Prime, Regular Polygon, Straightedge, Trigonometry Values Pi/17

References

Archibald, R. C. ``The History of the Construction of the Regular Polygon of Seventeen Sides.'' Bull. Amer. Math. Soc. 22, 239-246, 1916.

Archibald, R. C. ``Gauss and the Regular Polygon of Seventeen Sides.'' Amer. Math. Monthly 27, 323-326, 1920.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 95-96, 1987.

Bishop, W. ``How to Construct a Regular Polygon.'' Amer. Math. Monthly 85, 186-188, 1978.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 201 and 229-230, 1996.

Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 26-28, 1969.

De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly 98, 97-108, 1991.

Dixon, R. ``Gauss Extends Euclid.'' §1.4 in Mathographics. New York: Dover, pp. 52-54, 1991.

Gauss, C. F. §365 and 366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. New Haven, CT: Yale University Press, 1965.

Hall, T. Carl Friedrich Gauss: A Biography. Cambridge, MA: MIT Press, 1970.

Klein, F. Famous Problems of Elementary Geometry and Other Monographs. New York: Chelsea, 1956.

Ore, Ø. Number Theory and Its History. New York: Dover, 1988.

Rademacher, H. Lectures on Elementary Number Theory. New York: Blaisdell, 1964.

Richmond, H. W. ``A Construction for a Regular Polygon of Seventeen Sides.'' Quart. J. Pure Appl. Math. 26, 206-207, 1893.

Smith, L. L. ``A Construction of the Regular Polygon of Seventeen Sides.'' Amer. Math. Monthly 27, 322-323, 1920.

Stewart, I. ``Gauss.'' Sci. Amer. 237, 122-131, 1977.

Tietze, H. Famous Problems of Mathematics. New York: Graylock Press, 1965.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. New York: Viking Penguin, 1992.

Yates, R. C. Geometrical Tools. St. Louis, MO: Educational Publishers, 1949.