Trigonometry Values Pi/17

Rather surprisingly, trigonometric functions of $n\pi/17$ for

an integer can be expressed in terms of sums, products, and finite root extractions because 17 is a Fermat Prime. This makes the Heptadecagon a Constructible, as first proved by Gauß.

Although Gauss did not actually explicitly provide a construction, he did derive the trigonometric formulas below using a series of intermediate variables from which the final expressions were then built up.

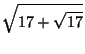$\displaystyle \epsilon$	$\textstyle \equiv$	$\displaystyle \sqrt{17+\sqrt{17}}$
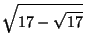$\displaystyle \epsilon^*$	$\textstyle \equiv$	$\displaystyle \sqrt{17-\sqrt{17}}$
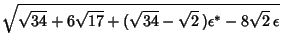$\displaystyle \alpha$	$\textstyle \equiv$	$\displaystyle \sqrt{\sqrt{34}+6\sqrt{17}+(\sqrt{34}-\sqrt{2}\,)\epsilon^*-8\sqrt{2}\,\epsilon}\,$
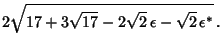$\displaystyle \beta$	$\textstyle \equiv$	$\displaystyle 2\sqrt{17+3\sqrt{17}-2\sqrt{2}\,\epsilon-\sqrt{2}\,\epsilon^*}\,.$

$\sin\left({\pi\over 17}\right)= {\textstyle{1\over 8}}[34-2\sqrt{17}-2\sqrt{2}\... ...{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\,\epsilon}\,]^{1/2}$
$\qquad \approx 0.18375$
$\cos\left({\pi\over 17}\right)= {\textstyle{1\over 8}}[30+2\sqrt{17}+2\sqrt{2}\... ...{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\,\epsilon}\,]^{1/2}$
$\qquad \approx 0.98297$
$\sin\left({2\pi\over 17}\right)= {\textstyle{1\over 16}}[136-8\sqrt{17}+4\sqrt{2}(1-\sqrt{17})\epsilon^*+16\sqrt{2}\,\epsilon$
$+2(\sqrt{2}-\sqrt{34}-2\epsilon^)\sqrt{34+6\sqrt{17}+(\sqrt{34}-\sqrt{2})\epsilon^-8\sqrt{2}\epsilon}\,]^{1/2}$
$\qquad \approx 0.36124$
$\cos\left({2\pi\over 17}\right)= {\textstyle{1\over 16}}[-1+\sqrt{17}+\sqrt{2}\... ...sqrt{68+12\sqrt{17}-2\sqrt{2}(1-\sqrt{17}\,)\epsilon^*-16\sqrt{2}\,\epsilon}\,]$
$\qquad \approx 0.93247$
$\sin\left({4\pi\over 17}\right)= {\textstyle{1\over 128}}(-\sqrt{2}+\sqrt{34}+2\epsilon^*+2\alpha)$
$\times\sqrt{68-4\sqrt{17}-2(\sqrt{34}-\sqrt{2}\,)\epsilon^+8\sqrt{2}\,\epsilon+\alpha(\sqrt{2}-\sqrt{34}-2\epsilon^)}$
$\qquad \approx 0.67370$
$\sin\left({8\pi\over 17}\right)= {\textstyle{1\over 16}}[136-8\sqrt{17}+8\sqrt{... ...\sqrt{34}-3\sqrt{2})\epsilon^-2\beta(1-\sqrt{17}-\sqrt{2} \epsilon^)\,]^{1/2}$
$\qquad \approx 0.99573$
$\cos\left({8\pi\over 17}\right)= {\textstyle{1\over 16}}(-1+\sqrt{17}+\sqrt{2}\,\epsilon^-2\sqrt{17+3\sqrt{17}-\sqrt{2}\,\epsilon^-2\sqrt{2}\,\epsilon}\,).$
$\qquad \approx 0.09227$

There are some interesting analytic formulas involving the trigonometric functions of $n\pi/17$ . Define

$\begin{eqnarray*} P(x)&\equiv&(x-1)(x-2)(x^2+1)\\ g_1(x)&\equiv& {2+\sqrt{P(x... ...r 4}}[g_i(x)-1]\\ a&\equiv& {\textstyle{1\over 4}}\tan^{-1} 4, \end{eqnarray*}$

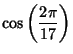$\displaystyle f_1(\tan a)$	$\textstyle =$	$\displaystyle \cos\left({2\pi\over 17}\right)$
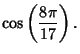$\displaystyle f_4(\tan a)$	$\textstyle =$	$\displaystyle \cos\left({8\pi\over 17}\right).$

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 192-194 and 229-230, 1996.